Rearranged Rectangle

We had several solutions for this task.

Ella and Samuel from St Mary's Church of England Primary School in Woodbridge sent in the following:

When the blocks 1 and 2 are together it's really helpful because it's making 3. Also, if you switch the 6 block around each way then it gives you more solutions.

I found that every shape that you make you can add a really small change and you have a lot of possibilities (I haven't drawn them all as that would take forever!).

Here are four solutions from Douglas Road School in Canada:

Yiling

Juna

Mikayla

To solve the problem, I need to know what a rectangle is. A rectangle has two parallel sides from each other. A rectangle also is a quadrilateral with four sides that meet at ninety degrees angles. So that means a square counts too!

At first my method was to make as many rectangles as I could. But then I realised I made too many rectangles and their perimeters were all the same. So, my new method was to still make as many rectangles as I could but, with different perimeters.

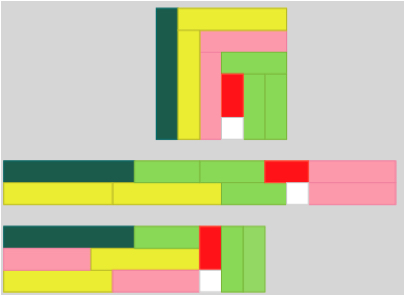
Here are some examples of my rectangles that I think are the only ones that really count. I made 3 rectangles, including 1 square. My idea I had was thinking of the factors of 36 because 6 x 6 (which is the width and length of the original rectangle) = 36. So, the factors of 36 are 1, 2, 3, 4, 6, 12, 18 and 36.

Jasnin

In my class I did a math problem called “The Rearranged Rectangles.” The topic of the problem is “How many different rectangles can I make using the rods from the problem?”

It means I must make as many rectangles as I can using the rods from the problem. However, the area of the rectangles I made does not affect the case of the dimensions. Like if all sides are even and I made another rectangle like that, but the rods are not in same spot as the other one, it doesn't count.

It wasn't straightforward making the rectangles. But as I progressed and made big long ones, things got easier and efficient since I understood the problem more, and I got a method. My method was to try different lengths. So, if I had one rectangle with a side equal to four white rods, I would try to do another rectangle with a side equal to three white rods. The more rectangles I created with the rods, the harder it was to find different ways to make more because when you have a lot it's hard to find more.

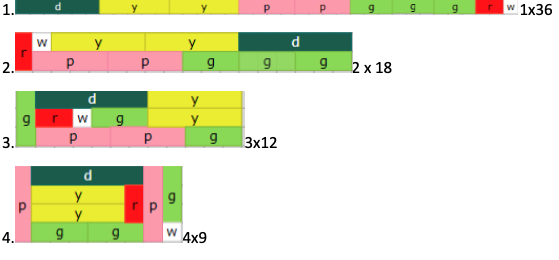
Well done, these are excellent solutions. They do show though, that the word "different" may not mean the same thing to everyone. We have different rectangles in their length, width and perimeter. We have different rectangles according to the makeup of the cuisenaire pieces used.

Did you discuss this when you tried the task? How did you decide what 'different' means in this problem?