Picture Your Method

Thank you to everyone who sent in their ideas for calculating 18 x 5.

Clearly, the answer is definitely not the most interesting part of this problem! Much more interesting is thinking about the way you arrived at your answer. In the problem we suggested five possible ways to find the answer, and we challenged you to match each of those ways with their correct diagram.

Simran, from Maurice Hawk School in the USA, shared the following list of matched calculation methods and diagrams:

A Jamie

B Neil

C Sammi

D Ricardo

E Bryan

Simran also shared her preferred method: 

My method was the same as Sammi's method. I used the distributive property to solve this problem. I separated 18 into 8 and 10, found the products of 5 X 8 and 5 X 10 and added the two products to get 90 like Sammi did.

Rachel, from Burrough Green School, sent in this video explaining her reasoning for each pair of cards:

Well done, Rachel!

We shared our five diagrams with you, but there's other ways to explain your reasoning too. Rachel decided to use cubes to explain why one of the methods works:

We also challenged you to think about other ways you could calculate 18 x 5.

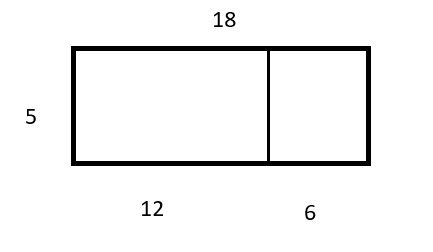
Lachlan, from Full Spectrum Education in Australia, shared his method and diagram:

I split 18 into 12 and 6, then I multiplied 12 x 5 (=60) and 6 x 5 (=30) and then I added the answers together.

My diagram:

Krishna, from the CS Academy in India, shared this photo of another method for calculating 18 x 5:

First I took 5 and partitioned it into 3 and 2.

Then I took 18 and multiplied it by 3, and 18 x 3 = 54.

Then I took 18 again and mulitplied it by 2, and 18 x 2 =36.

Then I took 54 and added it to 36, which is equivalent to 90.

Do you think you could draw a sketch to represent Krishna's method visually?

Krishna also shared another way for calculating 18 x 5:

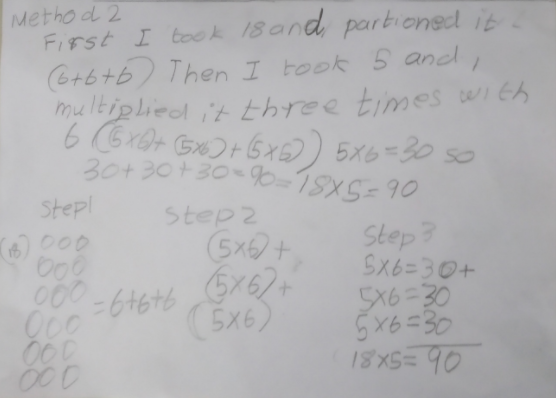
First I took 18 and partitioned it into 6, 6 and 6.

Then I took 5 and multiplied it three times with 6.

5 x 6 = 30 so 30 + 30 + 30 = 90.

Simran also thought about different ways to partition 18:

We can also separate 18 in different ways, one way is shown here:

Very well done to you all!