True or False?

Thank you to everybody who sent in their ideas for this task. We received a lot of solutions from children at the British International School in Vietnam and from children at the ABQ Education Group in Oman, as well as children at Pierrepont Gamston Primary School in England. Well done to those children and to everybody else who sent in their reasoning for why each number sentence was true or false.

Juyeong from Nord Anglia School Jakarta in Indonesia explained the technique they used to solve the questions:

I solved them using the things that I already know and the things that I already can do.
What I know that will be useful to solve it is that = means the same and 19 + 15 which is the basic adding of this question is 34.

Well done Juyeong - with questions like these, it can be really helpful to think about which facts we already know.

Avneet from Pierrepont Gamston Primary School worked out all the combinations of two numbers that add up to 34:

Questions 1-6 are all correct. I have concluded that the only possible solutions for _+_=34 (without decimals or negative numbers) must be 1+33, 2+32, 3+31, 4+30, 5+29, 6+28, 7+27, 8+26, 9+25, 10+24, 11+23, 12+22, 13+21, 14+20 and 15+19. This is why questions 7, 9, 10 and 11 are wrong and 8 and 12 are right.

This is a really interesting way of thinking about it, Avneet. Have a look at these additions - can you see any other ways of making 34?

Gracie and Georgie from Horfield CEVC Primary School in the UK have looked closely at how adding and subtracting from two numbers can keep the total of the numbers the same:

Thank you both for sending us your ideas. Have a look at the rest of Gracie and Georgie's solutions for some very clear explanations of why each statement is true or false.

Anika from Holy Family Catholic Primary School in England has used some similar strategies to Gracie and Georgie. Anika has also looked at the last digits of each of the numbers to decide whether the calculation can be true or not:

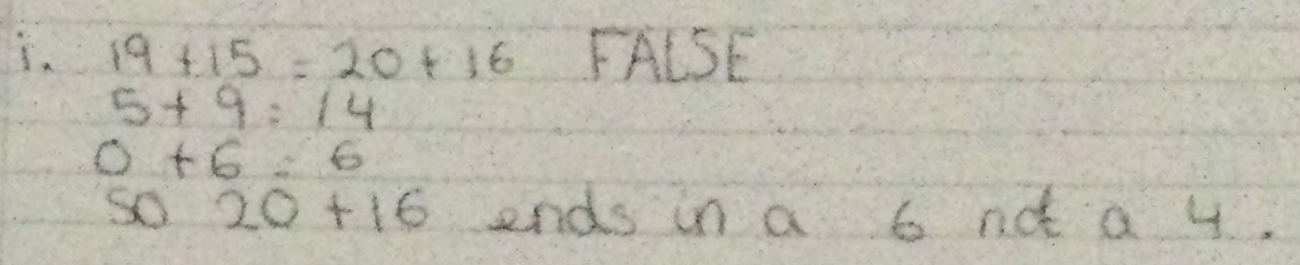
Thank you for sending us your ideas - we've uploaded a picture of the rest of Anika's solutions.

Jannah from the ABQ Education Group sent us this video explaining why each number sentence is true or false in the extension activity:

Jannah also explained that the video got cut off before the end, but that the last number sentence has to be false because the two numbers on the left aren't very big numbers so they can't possibly equal 2041. Thank you for that video, Jannah!

Isabelle from Nord Anglia School Jakarta has also used looked at the size of the numbers to answer some of these questions:

a. True, because 346 + 3 = 349, and 289 - 3 = 286, so both of the answers of the equation will be equal = 635 (346 + 289 = 349 + 286).

b. True, because they are the same equations, they just swapped the numbers' order. So, 727 + 581 = 581 + 727 = 1,308.

c. True, because 478 + 2 = 480, and 192 + 2 = 194, so the answers will be the same or equal, 478 - 192 = 480 - 194 = 286.

d. False, because the equation on the left will have a smaller answer, because 831 is smaller than 841, but the 344 is greater than 334, so the answer for the equation on the left will be smaller than the answer for the equation on the right. (831 - 344 = 487 is smaller than 841 - 334 = 507).

e. False, because the first sum on the left will have a greater number, because 346 is greater than 345, and 289 is greater than 288, so 346 + 289 = 635 is greater than 345 + 288 = 633.

f. True, because 581 - 581 = 0, so 727 + 0 = 727.

g. False, because -344 + 346 = 2, so it means that 831 + 2 = 833 not 831 and you can also say that -344 + 346 = 2, not 0.

h. False, because 169 + 672 is definitely less than 1,000; the answer would be 841. So, 169 + 672 = 841, not 2041.

Well done Isabelle!

Luay from Goldsworth Primary School in the UK used real-life examples to explain some of the questions:

Q6) 727 + 581 - 581 = 727
A6) True. My sister has y amount of chocolates. I have x amount of chocolates. I put my x amount of chocolates next to my sister's y amount. Then I take my x amount of chocolates back home for no actual reason. So she has her original y amount left.

Q7) 831 - 344 + 346 = 831
A7) False - There is z amount of chocolates. 344 is taken away from that and 346 is added back which 2 more than what was taken away. So z becomes z + 2 which means you would have 2 chocolates more than what you had
initially.

This is a really helpful way of imagining what it means to do a combination of adding and subtracting in a number sentence - well done.

We also had an excellent solution sent in by Simran from Maurice Hawk School in the USA. Thank you again to everybody who sent in their ideas for this challenge.