Data Duos

Here are four shapes (they are labelled A, B, C and D):

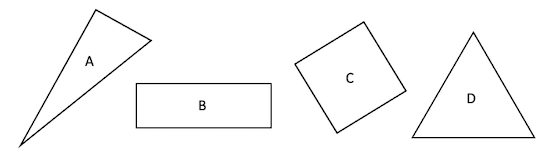
What do you notice?

In how many different ways could you sort the shapes?

Kerstin sorts the shapes in three different ways. 
She creates a Venn diagram and a Carroll diagram for each way of sorting.

Here are the three Carroll diagrams she makes...

Carroll number 1:

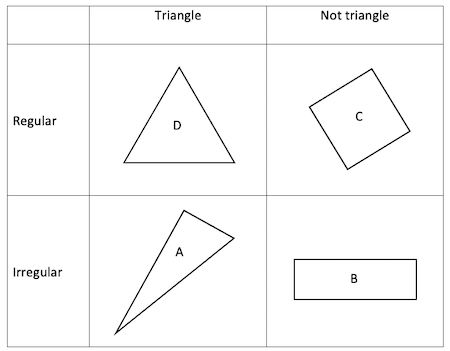
Carroll number 2:

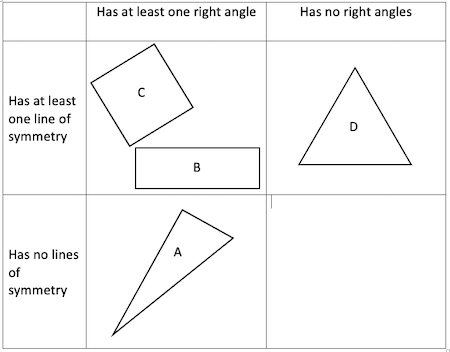
Carroll number 3:

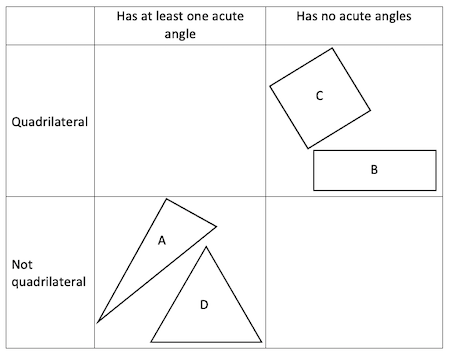
Here are the three Venn diagrams, but she hasn't labelled them yet.

Venn number 1:

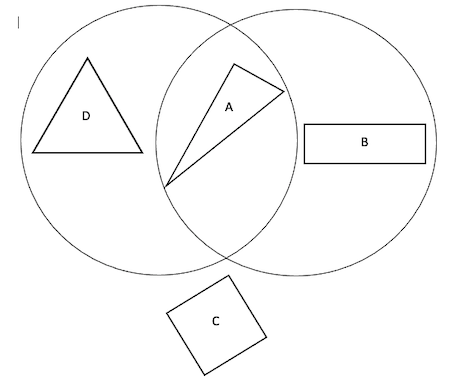
Venn number 2:

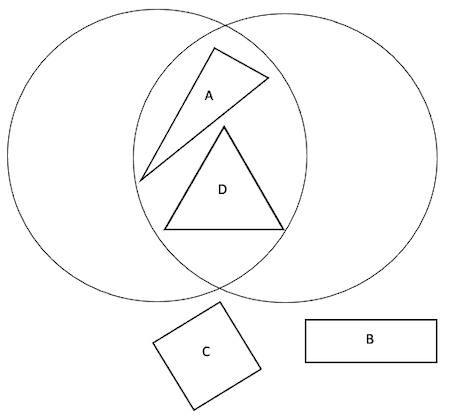
Venn number 3:

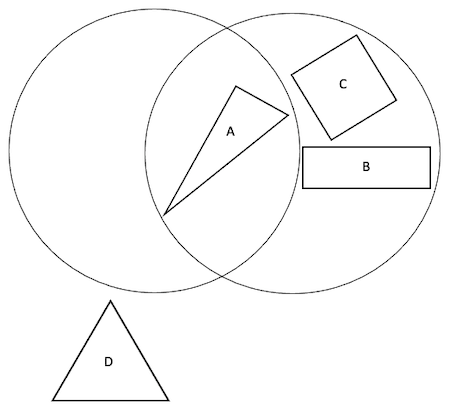
Can you match the Carroll diagram to the Venn diagram showing the same way of sorting the shapes?
Can you add labels to each Venn diagram?

We would love to hear about how you approached this task.

You may find it helpful to print out this sheet which has copies of all six diagrams on it.

This task was inspired by a 2009 SATs question.