Going Deeper: Achieving Greater Depth in the Primary Classroom

As a mastery approach becomes increasingly common in many schools, we have been working with teachers on a project to uncover effective ways to support their learners working 'at greater depth'. In this article, we will share our key findings and some of our favourite whole-class teaching resources which offer opportunities for teaching 'at greater depth'. (Several of these are linked from the NCETM's resources which exemplify their 'ready to progress criteria'.)

Teaching at 'greater depth'

One of the challenges facing many teachers is engaging all learners throughout the lesson when adopting a whole-class teaching approach. As guidance issued to schools indicates, "It is inevitable that some pupils will grasp concepts more rapidly than others and will need to be stimulated and challenged to ensure continued progression” (Askew et al., 2015, p.6).

Aware of these concerns, the guidance adopted the phrase ‘mastery at greater depth’ and suggested that pupils working at this level should be able to:

• solve problems of greater complexity (i.e. where the approach is not immediately obvious), demonstrating creativity and imagination;

• independently explore and investigate mathematical contexts and structures, communicate results clearly and systematically explain and generalise the mathematics.

(Askew et al. 2015, p.7)

The requirement for learners working 'at greater depth' to investigate more complex problems, work independently and communicate their ideas to others are the very foundations of our Low Threshold High Ceiling (LTHC) approach at NRICH: a low threshold ensures that every learner can get started on a problem and the high ceiling ensures that there is a suitable level of challenege, often unseen, for the learner to consider if and when they are ready to do so.

We teamed up with a group of schools based in Tower Hamlets, who were participating in a joint professional development programme with NRICH and the Tower Hamlets Education Partnership, to invesigate ways to maximise the potential of our curriculum-mapped LTHC resources for teaching 'at greater depth'. In this article we share some of their top tips.

Be prepared to be surprised

Some of our project teachers reported discovering previously unseen problem-solving abilities among their learners when using LTHC teaching resources with their classes. More specifically, some learners who were not engaged by other aspects of the primary mathematics curriculum thoroughly enjoyed opportunities to explore and investigate their own ideas. One of the activities they explored is Domino Sets, in which they are asked how they would check that a box of dominoes contains a full set.

During a visit, we joined a very engaged class who quickly got started on the challenge. Working in pairs, with their teacher taking reguar opportunities to pause the groups and allow time to share their ideas with the wider class, the learners began to organise their dominoes so that they could more easily check which, if any, were missing. Some learners who had completed the initial task were further challenged to consider how many dominoes they might have if the maximum number of dots on each side was increased to seven:

Teacher: We’re doing the seven row. Prove to me that there’s eight in the seven row.

Learner: It will only be like this, seven zero add one, seven one, seven two, seven three, seven four, seven five, seven six, seven seven but you can’t go over that.

Teacher:  So when you get to the seven seven you can’t go any further. So you proved it. There’s no doubles and you can’t go any further than seven seven, can you?

The learning did not stop there, the lesson went much deeper as the learners were encouraged by their teacher to set themselves the challenge of thinking about sets of dominoes which go up to 'double 10', or 'double 20' or even 'double 100'. Working with these much larger domino sets encouraged those working 'at greater depth' to generalise their ideas, and their enthusiasm led them to continue working through their break time! 

Reflecting on the lesson, the teacher noted that one member of that day's 'at greater depth' group had previously struggled to engage with their mathematics:

What’s great about NRICH activities is that it just shows children can shine even if we’ve got them in a box under 'expected'. That’s what I love about it... You know, he completely steps out of the box and he’s shining.

Clearly, one of the many benefits of working with LTHC resources is their potential for challenging all learners and enabling them to reveal their potential. Be prepared to be surprised.

Encourage a growth mindset

No-one enjoys trying to do too much at once, any activity can become frustrating if it is too far beyond our comfort zone. This is true in our classrooms too. In our mathematics lessons, our curriculum challenges teachers to develop fluency, reasoning and problem-solving skills, and trying to find a balance within a particular lesson can be a challenge (this is an aspect we explore more fully in this article by Clare Lee and Sue Johnston-Wilder). By choosing LTHC activities, learners can easily get started on a task, building their confidence and willingness to engage with further challenges later on.

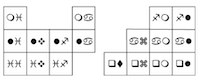For example, our Coded Hundred Square appears an easily understood task. It encourages learners to think about the construction of the familiar hundred square and about the first hundred numbers in our counting system by challenging them to piece together a hundred square which is written in code. However, learners may need to work on their resilience and perseverance skills as they will soon discover it is not quite as easy as it first appears! As they test out their ideas and become even more curious about the construction of this coded hundred square, this becomes an ideal activity for encouraging learners to work 'at greater depth' by offering conjectures, explaining and justifying their ideas. Here is Jordan and Juliana's thinking about their approach:

One of the strategies we used to solve the coded 100 chart was to look for patterns. We did this by looking in each column and finding that the symbols end with the same shape. For example, the first column of numbers always end in a rhombus shape. The same thing with the rows. Each row, we noticed while putting the symbols together, begins with the same shape. To solve this problem, we think it's best to work with the shape you first put in the 100 chart, and keep building off of that one. The first piece you out in the 100 chart works best if it fits into a corner of the chart.

In contrast, Nathan adoted a very different approach:

Start by placing any one piece and think which one will fit. Before putting it there, think if any other shape could fit.  Then, if not try another shape that could fit. After the one you choose is put on, repeat until the coded hundred chart is filled.  If you mess up, click on pieces to show the full piece and see if you can change a piece for another piece. Remember the first strategy to check if another one can fit after that one and then repeat again and again until you're done. After I fit the pieces together, I looked down each column. I checked that all the symbols in the ones placed matched. I looked across each row and checked that the symbols in the ones places were in order (1,2,3,4...).

Celebrate mathematical thinking

For learners to be working 'at greater depth', they need to be communicating their ideas clearly to others. In our project schools, the teachers often encouraged their learners to reflect on their problem-solving by recording their ideas in a class book. These books were proudly shared with visitors on arrival to their classes, including the NRICH team. Although we cannot visit every classroom, we do enjoy reading solutions to our problems. For example, Jordan, Juoiana and Nathan all submitted their ideas about the Coded Hundred Square to the team and their ideas were published on NRICH. Your classes are very welcome to share their ideas about our problem-solving tasks too, simply visit our Live Problems page for our very latest opportunities to communicate mathematically with the team. We publish a selection of the submissions we receive on our website.

An ideal problem for encouraging learners to share their mathematical thinking with others is The Deca Tree. This problem can give some substance to children's ideas on place value especially when you are introducing or using numbers greater than 1000. It shows in a pictorial way what the extra zeros 'do' to a number when multiplying by 10 and 100. We have found that learners develop several different ways to arrive at a solution. Here is Kirsty's approach which we published on NRICH:

There are 10 leaves per twig
There are 10 twigs per branch
10 leaves x 10 twigs = 100 leaves per branch
There are 10 branches per trunk
100 leaves x 10 branches = 1000 leaves per trunk
There are 10 trunks per tree
1000 leaves x 10 trunks = 10 000 leaves on the tree

Cut off one trunk: 10 000 - 1000 = 9000 leaves left
Cut off one branch: 9000 - 100 = 8900 leaves left
Cut off one twig: 8900 - 10 = 8890 leaves left
Pull off one leaf: 8890 - 1 = 8889 leaves left

There are 8889 leaves left on the tree.

Another learner called Rachel seemed to approach the problem in the same way as Kirsty, but she found the total number of leaves which had been pulled off the tree before finding the total number of leaves on the tree initially. 

Submitting solutions often leads to published solutions, and the teachers in our project schools also reported on the usefulness of the solutions accompanying our resources. Some teachers set aside time the following day after introducing an NRICH problem to their classes to enable their learners to compare their solutions with those from other classes:

I really like the solution thing now that I know how to use it and things. Getting the language out of it and stuff and using it after they’ve done it. Maybe tomorrow... we might start by looking at the solution that was there... Everyone will understand it tomorrow and then we can really, you know, look at it and decide whether we like it and pull it apart.

Allow time for you to think mathematically too

Another key finding from our project teachers was the importance of setting aside time to explore each LTHC activity for themselves before the lesson. This approach enabled the teachers to consider the possibilities for extending the learners where needed, to enable teaching 'at greater depth', but it was often seen as a thoroughly enjoyable experience too:

I mean, I consider myself greater depth, okay? ... I do have, you know, quite a high level of maths. So, basically, if I have a greater depth and I’m enjoying it and taking it on and forward progressing, clearly those children can do the same, can’t they?

Summary

Our school-based research revealed these four 'tips' for schools to support their learners working 'at greater depth' using NRICH tasks:

• Be prepared to be surprised
• Encourage a growth mindset
• Celebrate mathematical thinking
• Allow time for you to think mathematically too.

We hope that reading this article will inspire readers to explore the potential of using NRICH tasks to support their own learners working 'at greater depth'.

This project would not have beeen possible without the generous support of the team at the Tower Hamlets Education Partnership and the teachers who welcomed the NRICH team into their classrooms. We were delighted to share our findings at the British Society for Research into Learning Mathematics Day (BSRLM) Conference in November 2020 - you can access a copy of the accompanying research paper which was published in the BSRLM's Proceedings here.

References

Askew, A., Bishop, S., Christie, C., Eaton, S., Griffin, P. and Morgan, D. (2015). Teaching for Mastery: Questions, tasks and activities to support assessment. Oxford University Press.

Lee, C. and Johnson-Wilder, S. (2018). Getting into and staing in the Growth Zone. Retrieved from https://nrich.maths.org/13491