Getting Started with the Reassembling a Gene Interactivity

This advice complements the article If I Share, Will My Friends Share Too?

You can think of the interactivity a bit like a jigsaw. The pieces have to be fitted together in such a way as to form a coherent whole. If you try to simply guess where the pieces go, then it may take some time. You can get there faster by looking at the edges and thinking about where they might fit together. It is not enough to look at the very first and last digit of the pieces, since the overlap may actually be two or more digits in some cases. The original sequence was 25 digits long, so if you have found a sequence longer than 25 digits, it is not the one you're looking for!

Here is the image of a completed one:

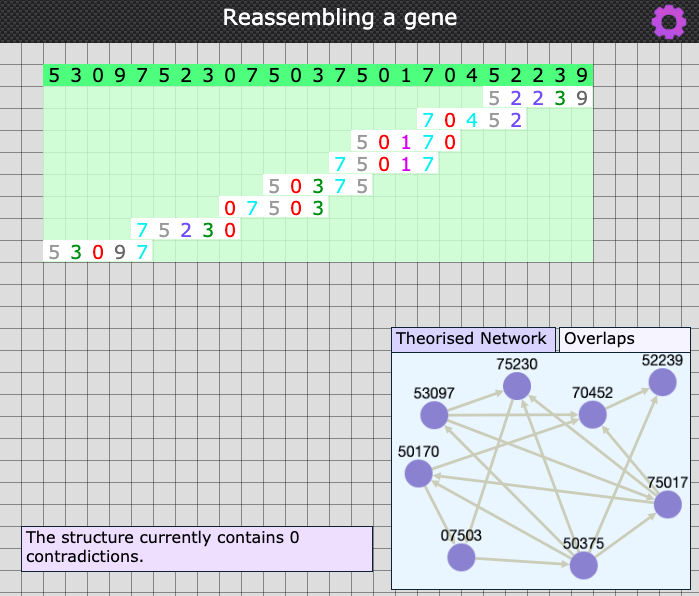
To help you, there is a graph visualisation tool in the lower right hand corner with two tabs that show different visualisations. The default setting is the 'Theorised Network' which reflects the network structure represented by the reads you've assembled into a theoretical structure. If the overlaps you propose are contradictory (having differing digits), then the computer will keep count of the number of contradictions.

The other tab is called 'Overlaps' and this looks at the reads currently available, and shows you a directed graph of overlaps which exist between them all. It looks a bit hectic, but it is worth looking at closely because it can give you an insight into which pieces are likely to fit where (you can zoom into it using your mousewheel if you have one). You know that each read needs to be used once, so the challenge is to find a way to 'walk' around the visualisation taking a route that visits each node once (a Hamiltonian path). You can move the nodes around to help you find a possible route.

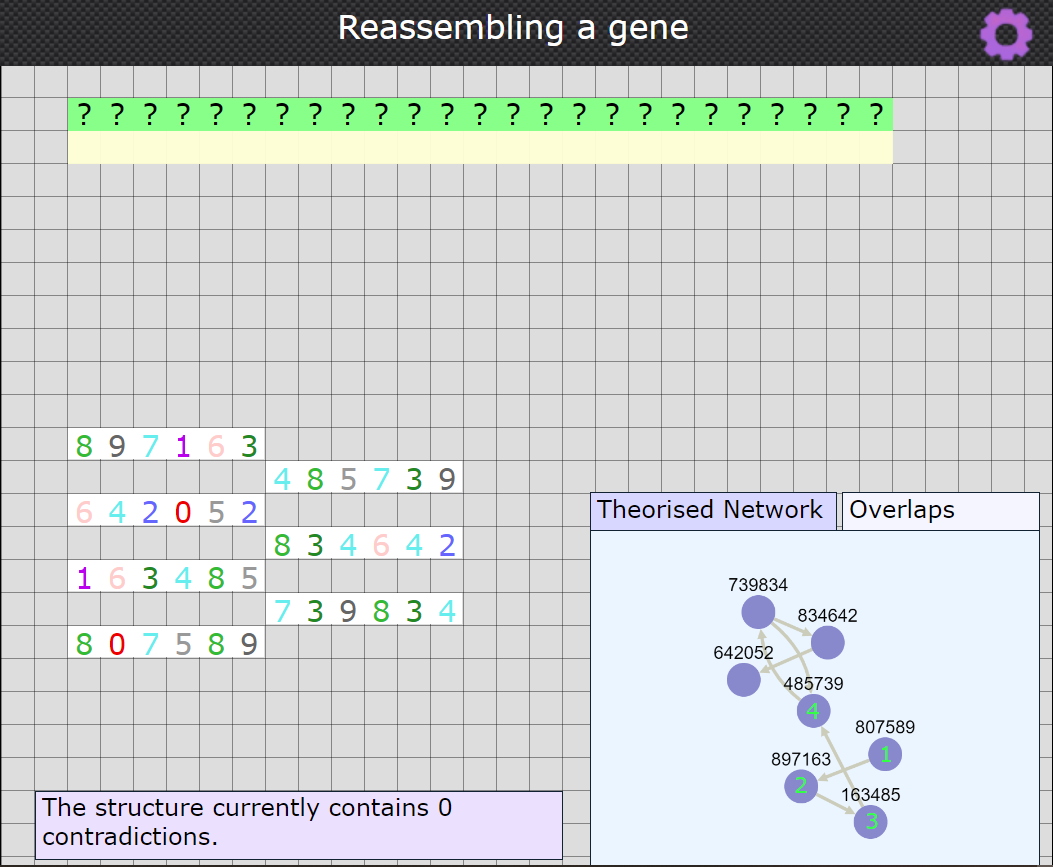
This example shows a set of reads which are easy to start off sequencing, because there is a node which has no possible precursor. 807589 must come first, because no other read overlaps with it at the beginning. 807590 can only possibly lead to 897163, with an overlap of "89". This example is a nice easy one! Usually the overlap networks have several more edges.

Bear in mind that if you have selected the option to introduce an error into the reads, one of the digits on one of the reads will be incorrect, and the corresponding overlaps will not show up in the visualisation.

If you are interested in learning more about how this technique is used in practice, and the reason why Eulerian cycles are more suitable for real sequences, this video is worth watching.