Solving by Squaring

Between the solutions we received, there was agreement that $x=-1$ was a valid solution, but some disagreement about whether $x=-4$ was a valid solution.

Marianna from Aiglon College in Switzerland decided that $x=-4$ is not a valid solution. This is Marianna's work:

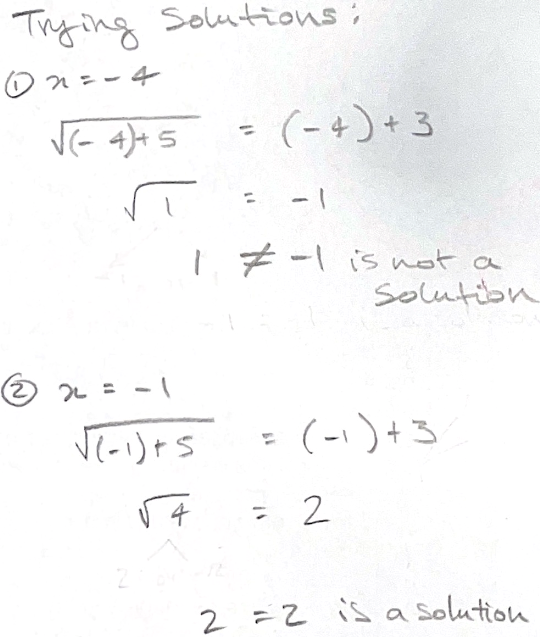
Alfie came to the same (correct) conclusion using logarithms:

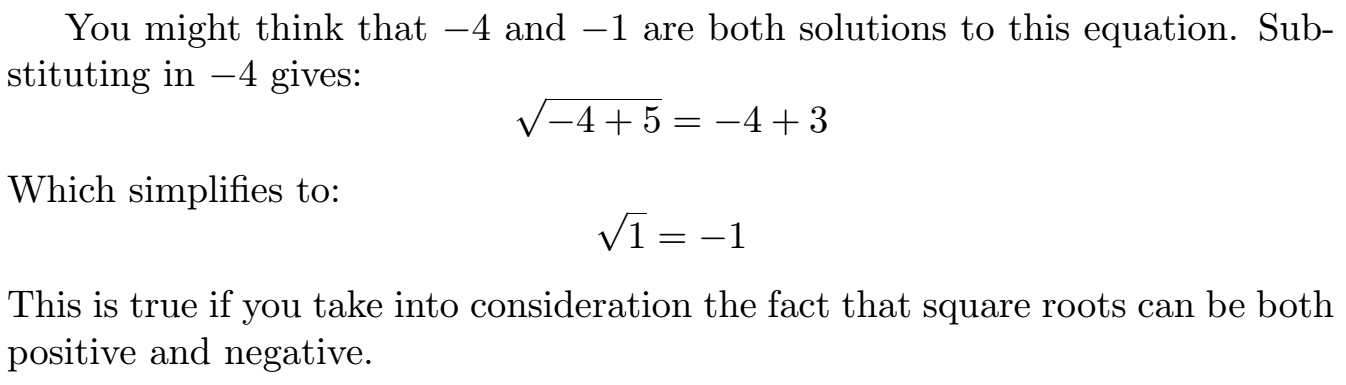
Marianna concluded:
(C) One solution is correct and the incorrect solution arises as a result of step (1)

While solution $x=-1$ works, $x=-4$ does not work. This is because when the equation is squared in step (1), the possibility of having a negative solution arises [that is, the possiility that $\sqrt{x+5}\lt 0$ arises]. However, when plugged back the positive square root does not allow a negative answer.

Shubhangee from Buckler's Mead Academy in England used graphs to explore this idea further:
The square root of 1 in the example is a type of one-to-one function, however the [incorrect solution arises by using the square root as] a case of one-to-many, which is not a function.

If we were to graph the original question using GeoGebra, then it would look something like this:

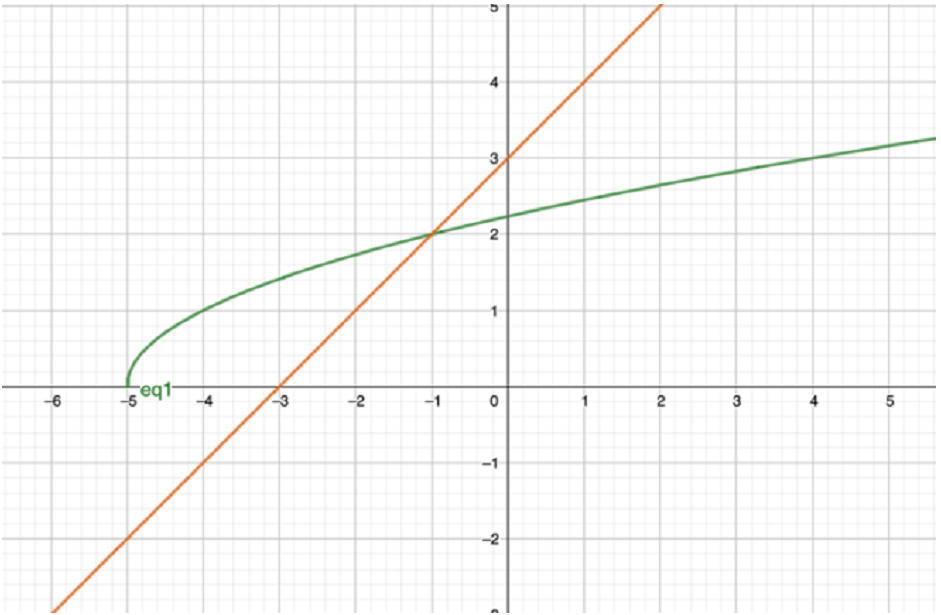
The green line is $y=\sqrt{x+5}$ and the orange line is $y=x+3$ and the point at which they intersect is $-1.$
This graph proves that the original question has only one possible solution.
The $-4$ result arises because we will always get a positive integer when we square numbers, even if they are negative.
Both $-4$ and $-1$ become a solution when we square both sides of the equation like we did in step (1), but if left in the original function form, then the question has only one solution which is $-1.$