Inequalities

Yazan from Dubai International Academy in the United Arab Emirates explained statement 1 must be true, assuming $a$ and $b$ are positive:

Statement 1 ($-b \ge -a$) is correct because $a$ has a higher value than $b$, so if you put a negative sign before both of them, $-b$ will be higher, because the higher the value of the number after the negative sign, the lower it is. Suspect a is $14$ and b is $10.$ If you compare $-14$ and $-10,$ the statement goes like this: $-14 \lt -10.$

Here is a diagram showing why the statement must also be true if $a$ and $b$ are both negative.

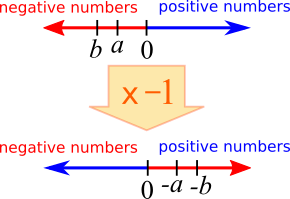
Here is a diagram showing why the statement must be true if $a$ is positive but $b$ is negative.

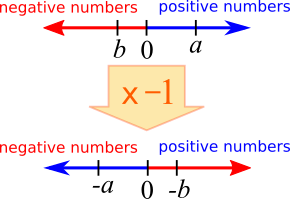
Terry and Miguel from International School of Krakow in Poland used a rule that comes from this idea. Terry wrote:

If you multiply or divide by a negative number, the direction of the inequality sign changes.

Yazan used an example to explain why statement 2 must be true:

Statement 2 ($a^2 + b^2 \ge 2ab$) is [correct] because two numbers squared can’t be [less than] the [product of] numbers by $2.$ Suppose $a$ is $7$ and $b$ is $3.$ $7^2$ is $49$ and $3^2$ squared is $9.$
$49+9=58,$ and $7\times3=21$ and $21x2=20,$ therefore, Statement 2 is [correct].

Terry and Miguel used algebra to show that statement 2 must always be true. This is Terry's work:

For the second argument, I began adding $-2ab$ to both sides, which made it $a^2-2ab+b^2\ge0.$ Knowing that $a^2-2ab+b^2$ can be expressed simply as $(a-b)^2,$ I changed the [inequality] into $(a-b)^2\ge0.$ The second argument is correct.

Naima from Bexley Grammar School and Vivek from Wilsons' School, both in the UK, gave examples to show that statement 3 is not necessarily true. Naima wrote:

We cannot say that statement 3 must be true. It will hold true if $c$ is positive - for example, if $a=4,b=2$ and $c=6,24\ge12.$

But if $c$ is negative, much like in statement 1 this will be reversed: if instead $c=-6,$ the expression will claim that $ac\ge bc,$ or $-24\ge-12,$ which is of course incorrect. So this statement will not be unconditionally true, despite $a$ being larger than $b.$

A single example is enough to show that a statement is not always true, so Naima and Vivek's examples are enough to show that it is definitely not true that statement 3 must be true. Miguel and Terry explained the same idea more generally. Miguel wrote:

Statement 3 is not always true as $c$ can be a negative number and therefore $bc$ would be greater than $ac.$