4 by 4 Mathdokus

Lots of children shared their tips for completing these Mathdokus - thank you all for sending in your ideas!

Tamsyn from Frederick Irwin Anglican School in Australia sent us this explanation:

One very helpful strategy for me is to use the the numbers in the top left corner. This helps me know which numbers are possible in each square so that I don't have to choose from as many options and the answer becomes clearer to me.

e.g. If multiplied together two numbers that have to equal 4, I know that it has to be a 4 and a 1. This is because I can't do 2x2 or something like that. I will also often find that the one has to go there because all the other squares that are in a row don't have a one which means that number needs to be a 4. This tells me that the other number is a one.

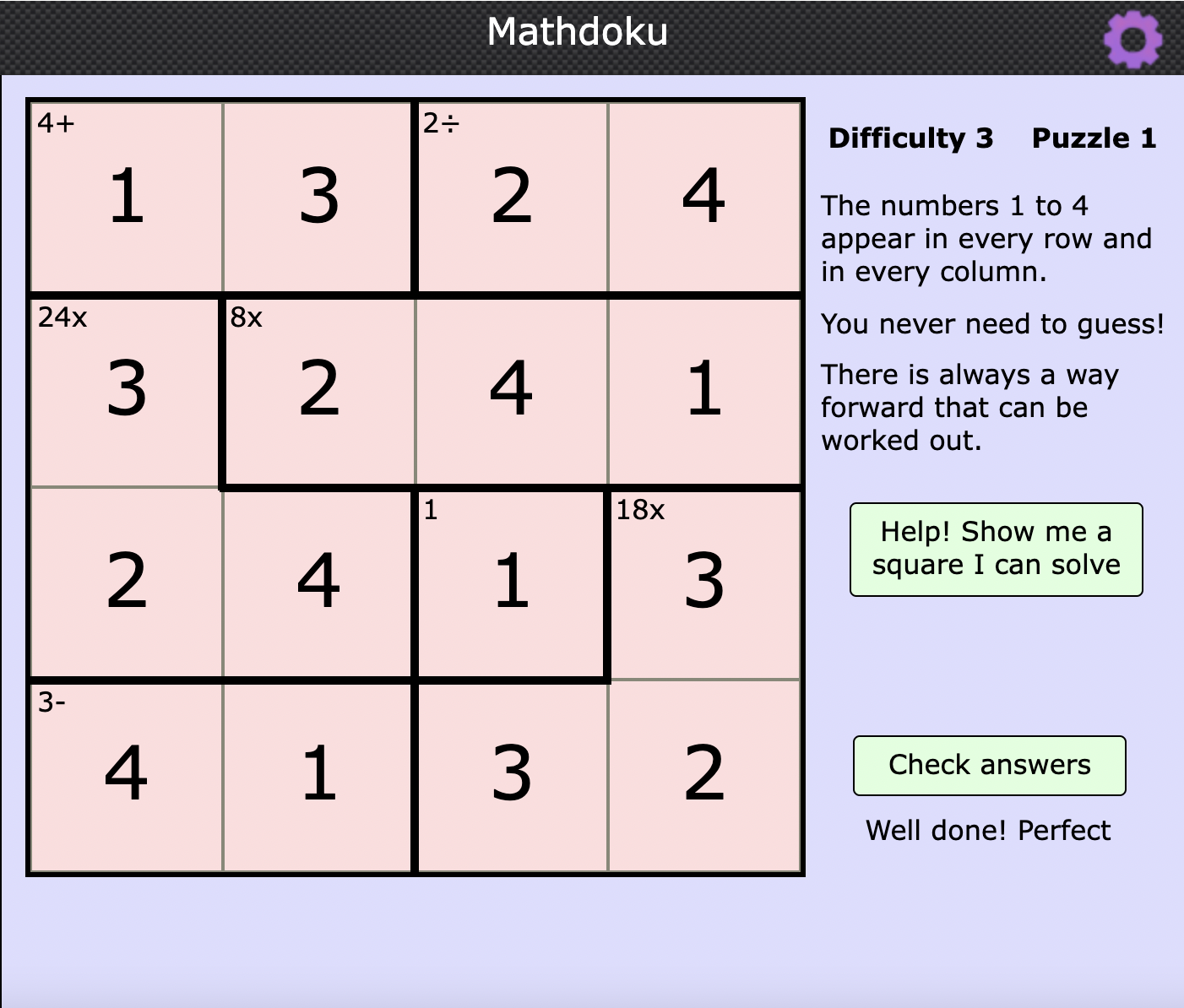
Good ideas, Tamsyn - often you can use the fact that you need the numbers 1, 2, 3 and 4 in every row and column to fill in some missing boxes. I wonder why it isn't possible to have 2 and 2 in a cage with 4x in the corner?

Uday from Pate's Grammar School in England sent in a solution explaining their first couple of steps. Have a look at Uday's PDF solution and see if you can work out what to do next after the third picture, using the general method that Uday describes.

Nicolas from St Charles Catholic Primary School in Ryde, Australia sent in an explanation of how to solve the first 4 by 4 Mathdoku. Take a look at Nicolas' full PDF solution and see if you can work out how to finish the Mathdoku by starting from the last picture on the first page and using the 'domino effect' that Nicolas talks about. Does this strategy work for all of the 4 by 4 Mathdokus? Have you spotted any Mathdokus where more strategies are needed to fill in all of the boxes without making any guesses?

We also received a step-by-step explanation for the first 4 by 4 Mathdoku from the children at the Maths' Big Questions club at Lady Margaret School in the UK. Have a look at the Maths' Big Questions club's full PDF solution. Can you see how they knew that the numbers they chose were definitely correct at every step?

We would love to hear from more of you! We are particularly interested to hear about any elegant strategies you used when you were stuck, and you think are worth sharing. Email us if there's a solution you'd like to share with us.