Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
5 by 5 Mathdokus



- Problem
- Student Solutions
- Teachers' Resources
Well done to Dhruv from St Ann's RC Primary in the UK and Bob Lam from West Island School who sent in correct solutions for Difficulty 1, Puzzle 1. This is Dhruv's work. Click on the image to see a larger version.
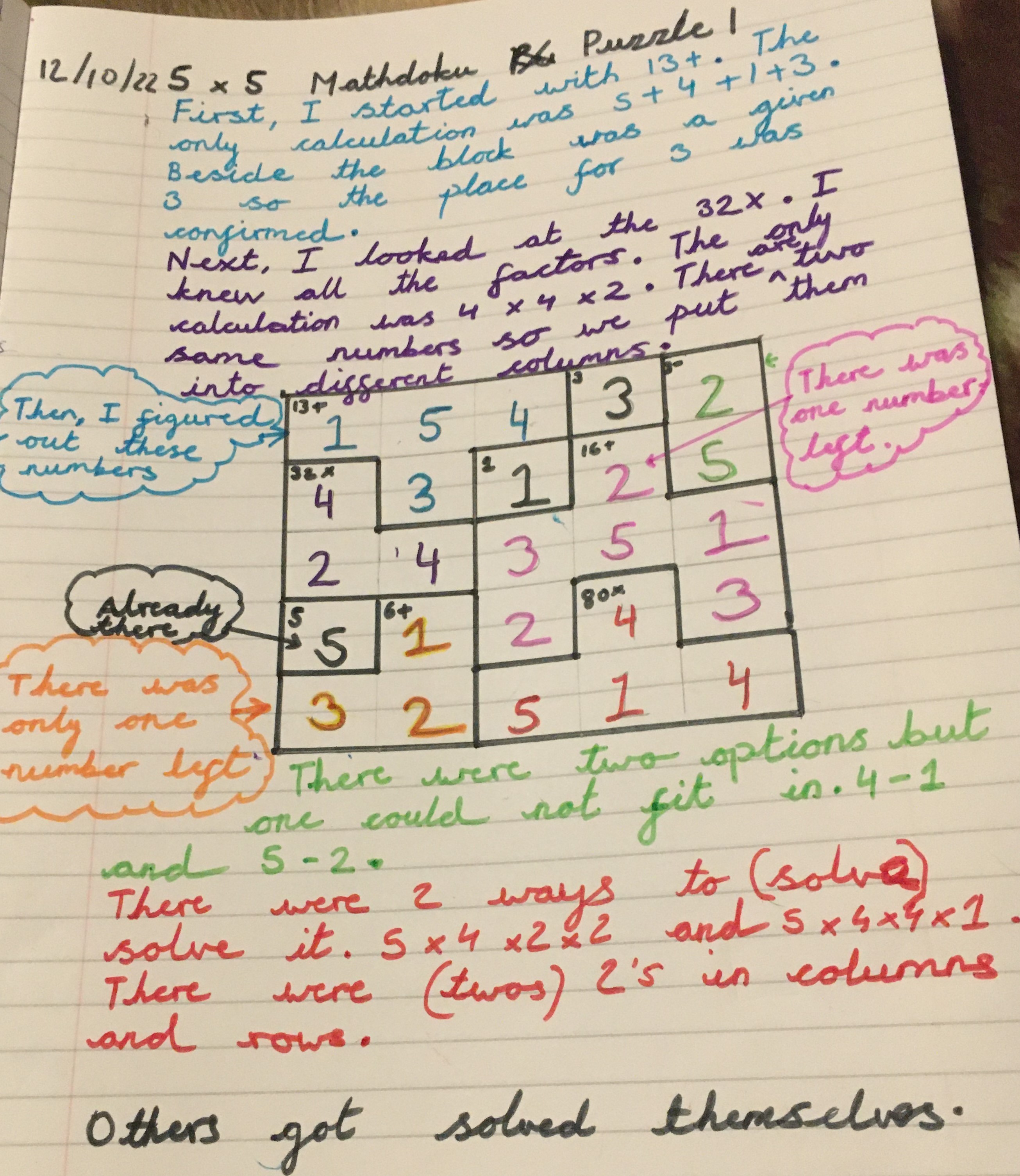
Carla from Aiglon College Switzerland, and Palestine, solved the same Mathdoku in a slightly different order, and gave more detail about each stage of reasoning. Click to see Carla's solution.
Then, I started from the (13+) cage. I started thinking of combinations of 4 numbers that would add up to 13. I ended up with 2 combinations that worked: 5,5,2,1 OR 5,4,3,1. So I wrote all the possible options for the numbers that could go in each square of the (13+) cage.
After that I went to the (32x) cage. We need to multiply 3 numbers to get a product of 32, so after writing down the prime factors of 32, I figured out that the only combination of 3 numbers that could give me 32 is 4x4x2. And since we can’t put 4 in the same line vertically or horizontally, the 4s have to be put diagonally in the cage, with the 2 in the third row (under the first 4 I put that is in the second row).
Then, I noticed that there were only two spaces left to fill in the first column, which were the first and last square in that column. And in order to complete the sequence of 1-5, I knew that these squares had to be filled with the numbers 1 & 3.
I decided to put 1 in the first empty square in the column, because it was already given to us that the number 3 is used in its row. As a result, the only last empty square left in the first column had to be filled with the number 3 to complete the 1-5 sequence.
Then, I went back to the (13+) cage, and eliminated all of the options that became impossible to use in the squares.
I then went to the (3-) cage, where I had to subtract two numbers to get 3. The only two combinations of numbers that worked were either 4&1 or 5&2, and since both number 4 and 1 were already taken in the second row, I knew I had to use 5 & 3, but I didn’t know in which order they had to be in yet.
I then went down to the (6+) cage, where 3 was already used in it and I needed two more numbers for all of them to add up to 6, which only left me with the number 1&2. But I still didn’t know which order I had to place them in either.
However, this gave me a clue that either way, the numbers 1&2 were already going to be used up in those 2 squares in that column, so I had to eliminate them as options in any of the other squares in that column.
This brought me back to cage (13+), where the only two options for the second square from the left in the first row were 5&2, but since I now knew the 2 was going to be used elsewhere, 5 was the only option. And for the square under 5, since 2 & 5 were already taken in that column, the only option left for it was 3. And therefore to complete the right combination of numbers that added up to 13, the last empty square in that cage (the third one from the left in the first row) had to be 4.
The only empty square left in the first row was now the last one (last one from the left/first one from the right), which had to be filled with 2 to complete the 1-5 sequence.
The square under it in the second row had to either be filled with 2 or 5 to complete the 1-5 sequence in that row, because these were the only two numbers missing. But since the number 2 was right above it, I knew it had to be 5.
Now there was only one empty square left in the second row, which was the second square from the right (next to 5) that had to be filled with 2 to complete the sequence.
After that I went down to the (80x) cage and started thinking of 4 number combinations that would give me the product of 80. I figured out after listing 80’s prime factors that the only 2 combinations that work are 5x4x2x2 OR 5x4x4x1. So I put in all the options possible in the squares in the cage.
Then, after eliminating all of the impossible values from each square, I realized the number 2 would only work if we put in the third square of the last row from the bottom right corner, because it was taken in every other column & row that crossed the cage.
So, since the combination (5x4x2x2) required two 2s for it to work, which was impossible to apply in this cage, I knew that I had to use the (5x4x4x1) combination. So once I eliminated 2 from that square, the only option left was 5. And since the rest of the options for the rest of the squares were only 4&4&1, I knew that the 4s had to be placed diagonally so they wouldn’t be in the same column or row, and the one had to be placed in between (in the second square in the last row from the bottom right corner).
Now, since 1 has been used in the last row, this allowed me to figure out the order I’m supposed to put the numbers in in cage (6+). So I put the number 2 in the second square of the last row in the bottom left corner because it was the only one missing from the 1-5 sequence anyway, and put the number 1 right above it for the cage to add up 6.
Now I only had the (16+) cage left. Firstly, in the third column, there were only two empty squares left that had to be filled with 2 & 3 to complete the sequence. And since 2 was already used in row 3 that crossed the empty square in column 3, I put the number two in the empty square under it (in row 4) because it wasn’t used in its row. I then put the number 3 right above it to complete the sequence.
In the 4th column there was only one empty square left in its middle, which had to be filled with 5 to complete the sequence.
And lastly, the last empty square in the third row had to be filled with 1 to complete its sequence, and the last empty square in the fourth row had to be filled with 3 to complete its sequence.
You’ll now notice that naturally, all the numbers we put in the cage (16+) add up to 16 even if I just relied on other numbers in the rows and columns that crossed it to solve it.
Thank you for taking the time to read my solution and I hope it helps!
Delilah and Amelia from Tockington Manor School in England described their strategy for Difficulty 2, Puzzle 1:
Firstly we put the numbers that it told us (5) into the square. We then started working out the corners, we knew that 15 had to be made by multiplying 1,5 and 3, we discovered that 40 had to be made by multiplying 2,4 and 5, 80 had to be made by multiplying 4,4, and 5 and 18 had to be made by multiplying 3,3 and 2.
We then fitted them into the grid like a sudoku puzzle, knowing that we had to have numbers 1-5 in every row, and filled in the gaps around the 5 in the middle, being careful not to have and overlap numbers in each row and column. For each number we made multiple combinations to make the number we had to make and we then tried different combinations until we came across something that did work. If we hadn’t done all of the separate parts separately then it would have been a lot harder.
Archie, Chole, Daniel, Ken, Noah and Skylar from Croydon Public School in Australia described their strategy:
The strategy used was to put all the possible numbers in the squares and slowly eliminate the answers that don't fit into the puzzle. We used the process of elimination combined with the guess and check strategy. We found this the best strategy and we also put all the possible answers in each square so that through elimination we knew which number was correct. We made sure that the numbers met the requirements of each problem and corrected the numbers if there were repeated numbers in each row and column.
You may also like
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?
It Figures
Suppose we allow ourselves to use three numbers less than 10 and multiply them together. How many different products can you find? How do you know you've got them all?
Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?