Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
6 by 6 Mathdokus



- Problem
- Student Solutions
- Teachers' Resources
Lucy from the UK, Carla from Aiglon College Switzerland and Palestine and Neel from Zurich International School in Switzerland both sent in their solutions with an explanation of their strategy.
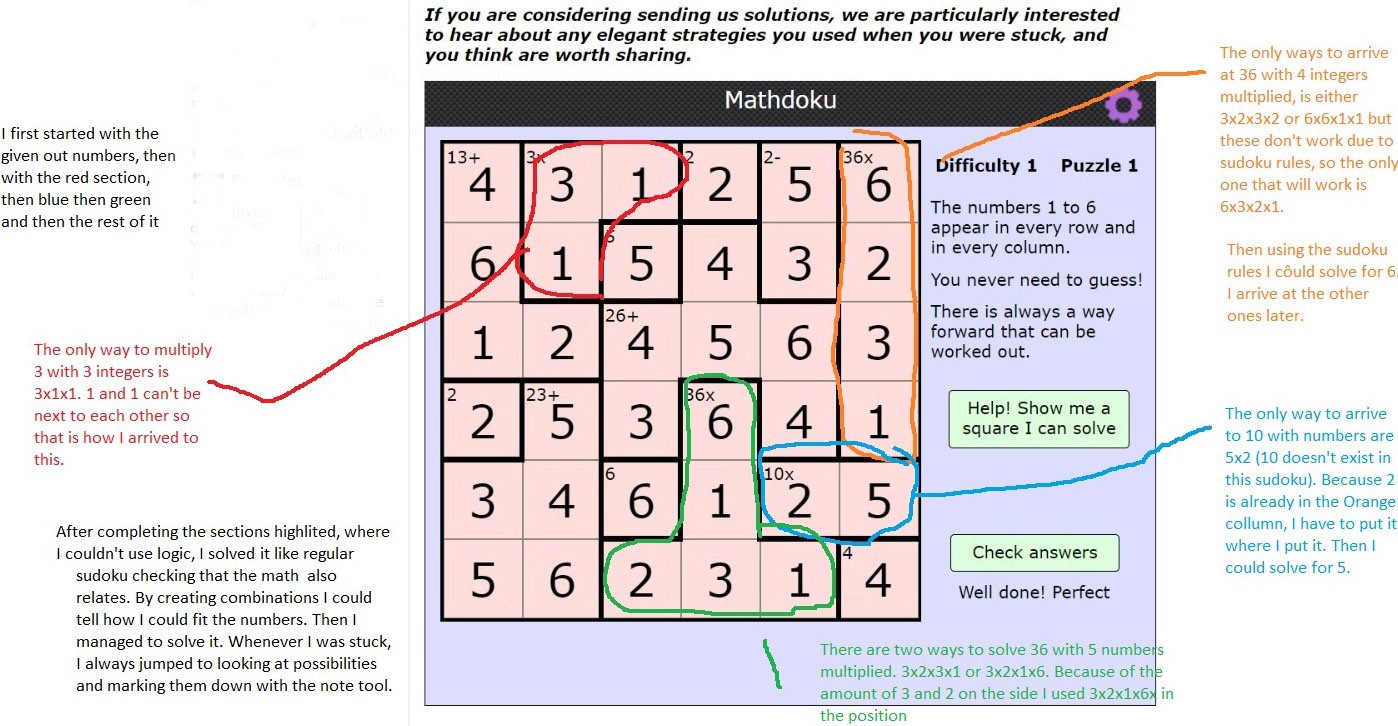
This is Neel's work on Difficulty 1, Puzzle 1. Click on the image to see it full size.
Carla also completed Difficulty 1, Puzzle 1 using a slightly different strategy. Click to see Carla's detailed solution:
Then I started thinking of the possibilities of two numbers with a difference of 2 for the cage next to the one I first solved. 3-1 would not work because the number 1 was already taken in both rows, so the only options left would be 5&3 OR 6&4.
Then I started thinking of a combination of 4 numbers that would have a product of 36 when multiplied for the cage right after, so I wrote down all of the prime factors for the number 36, and came to the conclusion that the only combination that worked was 1x2x3x6. For this first square in that cage (the first square in the top right corner), I figured its value had to be 6 because the numbers 1, 2 & 3 were already taken in that row. Which meant that the possibility of 6 & 4 (in that order) would not work for the (-2) cage that we saw before, because the 6 is now already taken in that row.
As for the rest of the values in the (36x) cage, the possibilities of second square from the top would be either 2 or 3 because 1 is already taken in that row), and for the third square it could be 1, 2 or 3, and for the fourth one it could be 1 or 3 (since 2 is already taken in that row).
I then went back for the (13+) cage in the top left corner. I figured the only two combinations of 4 numbers that would add up to 13 are: 5,4,3,1 OR 4,2,6,1. Since there is a 1 in both combinations, it was the first one I chose to place, and I placed it in the third square from the top because it was the only place where the number 1 wasn't already used in the same column or row. Then I wrote down all of the possible values in the rest of the squares from both combinations.
I then went down to the (10x) cage towards the bottom. The only two numbers that we can multiply for them to equal 10 are 5 & 2, and since I was certain that the number two was going to be used for the (36x) cage in the column on the right, then the number 5 had to be in that second square from the bottom right corner, and the number 2 had to be on its left.
After that i went down to the other (36x) cage towards the bottom, which I thought must’ve definitely had the same combination of numbers as the other (36x) cage because there are no other combinations of numbers that we could multiply to get 36 (the only difference in this one was that there were 5 values instead of 4 so we need to add an extra x1). So I listed all of the possible values (6, 3, 2 & 1) in each square while paying attention to what numbers are already used in their columns/rows. I then found that the only square I could put the number 2 in would be the third square from the bottom left, so I put the 2 there.
I then noticed that there were now only 2 empty squares in the top row, which were the first square from the left, and the second square from the right. Both of these squares' only possible values were either 5 or 4, so I need to find a way to eliminate one of these values from one of the squares to find the other one. So I started checking all of the possibilities for the squares in the top region… I then realised that in the (13+) cage, the only place the number two could go was in the square under the number 3 &1, and that it can’t be used anywhere else in that column because it was already taken in the other rows, so I put in the number 2.
This then allowed me to eliminate the number 2 from the list of options in the third square from the top right (in the 36x cage), which meant that the only place the number 2 could go from THAT column was in the second square from the top because it had nowhere else to go. And the only option for the square under it was now 3 since both 1 & 2 were taken in the same column/row. And the number under 3 had to be 1 because it was the only value left to complete the column with all values from 1-6.
Now, there were only 3 spaces left in the third row from the top, which could be substituted with the values 4, 5 and 6. In the first empty square from the right in that row (next to the number 2), the only value that would work for it would be the number 4 since 5 & 6 were already taken in that column. When I added 4 in, there was only one empty square left under it for that column, which had to be filled with the number 3 to complete the 1-6 sequence. This helped me figure out the value of the square right next to 3 (which is the same top square in the 36x bottom cage), because since 1 and 3 were now taken in that row, its value had to be 6. This meant that the number 6 could not go anywhere else in that cage, because it would mess up the (6x3x2x1x1) calculation which helped me eliminate the number 6 as an option from anywhere else in the cage.
I now knew that in the (26+) cage, the number in the middle of the cage (to the right of number 4) had to be 5 because 6 was now taken in its column, and therefore the one next to 5 had to be 6 to complete the 1-6 sequence.
Now going back to the first row, we now finally know that the option 6&4 cannot be used for the (-2) cage because I used 6 in that column, so it had to be 5&3 (5 in the top square, then 3 under it). And since 5 is now taken in the top row, the missing number in the first square from the top left (in the 13+ cage) had to be 4 to complete the 1-6 sequence.
The second number under 4 from the top left therefore had to be 6 because I already used 4 right above it and 3 in its row for (-2) cage solution.
There was now only one empty square in the second row from the top, which had to be filled with 4 to complete the 1-6 sequence.
Now everything becomes easier, because in the 4th row from the top, there are only 2 empty squares which have to be filled with either 4 or 5 to complete the sequence. The second empty square (in the 5th column) had to be filled with 4 because 5 is already used in the column, and therefore the only empty square left in the row = 5 (in the second column).
Then in the second column from the left, the numbers 4 & 6 are missing at the bottom to complete the sequence. So I put the number 4 in the 5th row (second empty square) because it is already used in row 6, and I put the number 6 right under it to have a completed sequence.
In the first column from the left, the numbers 3 & 5 are missing at the bottom to complete the sequence. So, I put in the number 3 in the only empty square left in row 5, and then the number 5 right under it to complete the sequence.
Now there are only 3 empty squares left. One in the 5th row, and two next to each other in the 6th row, all in cage (36x). In the only empty square in row 5, the only option left for that square is now 1 to complete the 1-6 sequence in that row. Then, the only option left for the square under it would be 3 to complete the sequence in that column AND to complete the (6x3x2x1x1) calculation. And finally, for the last empty square in row 6 cage (36x) (next to the number 3), I knew that it had to be 1 for it to again, complete the sequence in that column & row AND the (6x3x2x1x1) calculation.
Lastly, I’d like to give some general advice. Although this might sound obvious, I would strongly recommend typing out all options possible for each square rather than trying to memorise everything in your head, and do not put in any final answer unless you're completely certain of it, because it affects the entire Mathdoku.
Thank you for taking the time to read my solution and I hope it helps!
Lucy successfully completed Difficulty 2, Puzzle 2. This is Lucy's strategy:
When I was stuck, I looked for all the different permutations that were possible to make the amount needed with the numbers which I still had left.
I did that for all the cages which I didn’t have an answer for and then looked for the most likely numbers and any which couldn’t fit. Once I had done that, everything fitted into place all at once, because as each piece went into place it narrowed down all the other options. It helped to view it in two ways: a number of small problems which is the cages, and separately see it as a bigger problem and look at it all together.
You may also like
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?
It Figures
Suppose we allow ourselves to use three numbers less than 10 and multiply them together. How many different products can you find? How do you know you've got them all?
Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?