Seeing Parallelograms

Well done to everybody who managed to work out a winning strategy for this game. Freddie and Elliott from Richmond Methodist School in the UK sent in this image and description:

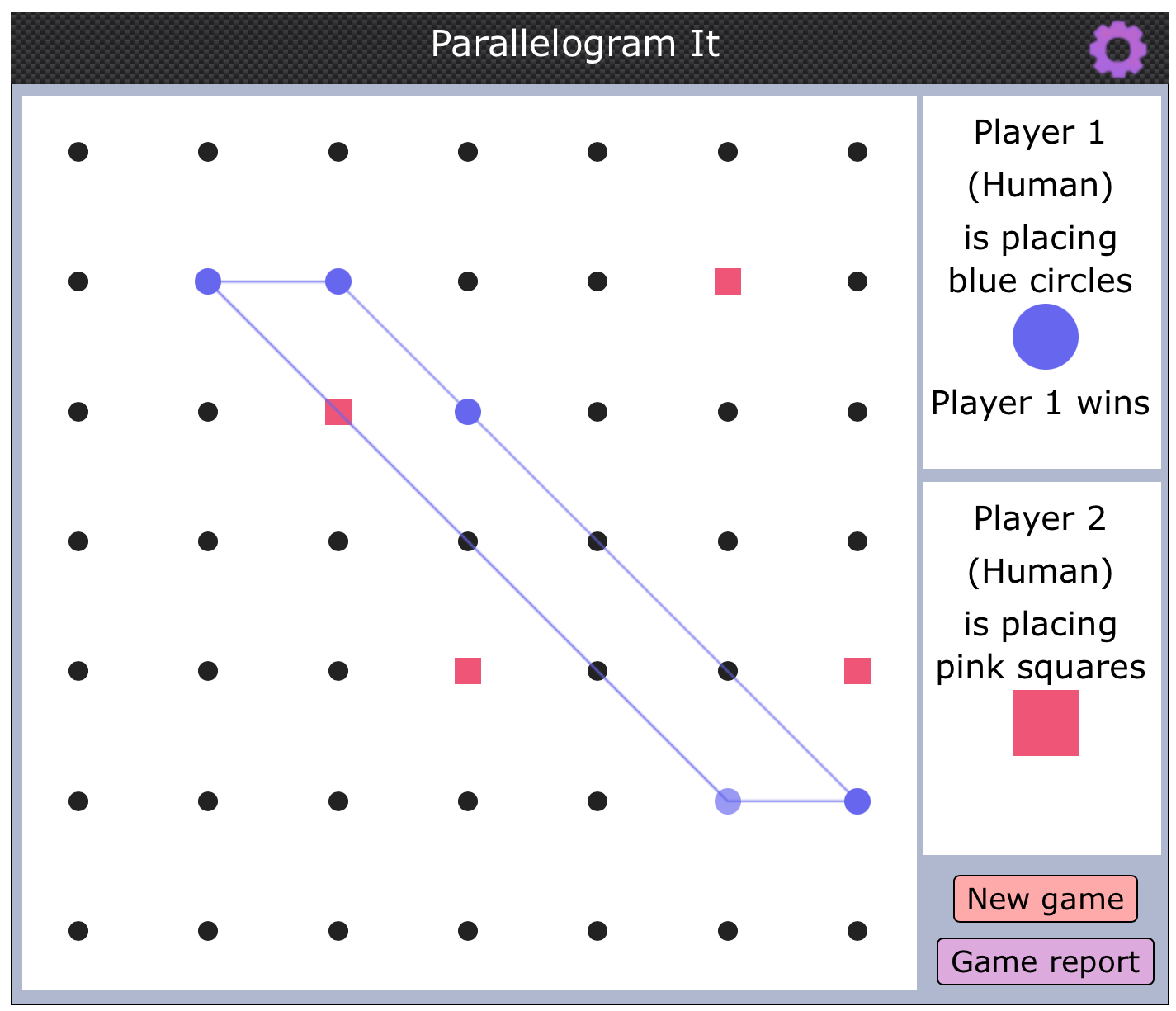
We played this game together. The picture above shows Elliott winning as Blue Circle but Freddie also won as Pink Square. It was really fun trying to beat each other and block each other's parallelograms. We also discovered that to trick your opponent you can make the shapes bigger than 4 consecutive squares.

I like your idea for tricking your opponent - you can make really long parallelograms that the other person might not notice before it's too late! I wonder if Elliott could have used a different strategy to win this game in fewer moves? 

We received lots of solutions from the children at Banstead Prep School in England, some of whom felt there was an unfair advantage to going first. Kaiyan, Josh and Dray shared their ideas:

In Maths we are looking at Seeing Parallelograms, there were tricks, cheats and strategies. Firstly you can use squares and rectangles which felt like cheating. And there were a few ways to always win.

This is unfair and should be fixed soon.

Although this game was really fun and I really enjoyed playing with my friends. The robot was a real challenge and was really hard to win against. You had to use your shape knowledge to figure out what the shapes really were. Going in the corners especially top left you win every single time. Which is pretty unfair.

It certainly is difficult to win against the computer, particularly when the computer goes first! I wonder if not being allowed to make squares or rectangles would make it more difficult for the first player to win?

Drayvian also pointed out that being Player 1 and starting in the top left at the beginning means that you can always win by making a small square, and they felt that this was a glitch rather than a legitimate way of winning. I agree that it looks suspicious that the computer player isn't trying to stop you from making this square in the top left hand corner. Here is an example of a situation in which Player 1 can win by making this square:

Looking at this picture, can you see why the computer player allows you to make the square? What is it trying to do in its final move?

I wonder if there's a different way to program the computer player. If the computer stopped you from making this square, perhaps in an earlier move, would you always be able to make another parallelogram or could the computer sometimes win?

Dhruv from The Glasgow Academy in the UK sent in this solution:

I like your method of trapping your opponent, Dhruv - it looks like you can be sure of making a parallelogram in one move from this position. I wonder if this is why it is impossible to beat the computer if it goes first? Can the first player always get into a position like this one in three moves?

Thomas from Banstead had a similar strategy, and described how Player 1 can win in four moves. We've tweaked the picture that Thomas sent in to make it slightly clearer. This was Thomas's explanation:

Within the rules, you can win by making a three wide, one high triangle and place one of your triangles to automatically win.

I have also noticed that you can also use other quadrilaterals to win, like a square or a rectangle. However, this strategy will only work if you go first, if you go second, you will always lose.

Here is my process for going first.

In step one, I place one triangle.

In step two, I place another two away.

In step three, I place one more in the middle, one upwards.

In step four, I place one to the opposite of where the computer has put his.

And the only next step is win.

Very clearly explained, Thomas! Harry, Zac and Avi from Banstead also sent in excellent explanations for how to win as Player 1 - thank you all for sharing your ideas with us.

Milan and Ryan also had some similar ideas for how to win by either making a square or making a triangle to turn into a parallelogram. Have a look at Milan and Ryan's solution to see how they did it.