Skip over navigation
Golden Powers , Golden Triangle and Golden Eggs.
Golden Ratio
Age 16 to 18
Challenge Level 
Why do this problem?
This problem introduces the Golden Ratio as the solution of a quadratic equation and links to many other investigations. A solution to the equation can be found by trial and error.Possible approach?
To motivate the topic why not introduce several problems where the students can discover that the Golden Ratio occurs in very different contexts and reinforce their own understanding of the algebra that occurs. For example:Golden Powers , Golden Triangle and Golden Eggs.
Key questions
If $\phi $ is the golden ratio then what is $\phi^2$ and $1 + {1\over \phi}$ and does this suggest a way to simplify the final equation?You may also like
Gold Again
Without using a calculator, computer or tables find the exact values of cos36cos72 and also cos36 - cos72.
Pythagorean Golden Means
Show that the arithmetic mean, geometric mean and harmonic mean of a and b can be the lengths of the sides of a right-angles triangle if and only if a = bx^3, where x is the Golden Ratio.
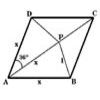
Golden Triangle
Three triangles ABC, CBD and ABD (where D is a point on AC) are all isosceles. Find all the angles. Prove that the ratio of AB to BC is equal to the golden ratio.