Skip over navigation
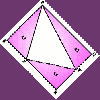
A Shade Crossed
Age 14 to 16
Challenge Level 
There were two solutions from Madras College, one from Thomas, James, Mike and Euan and the other from Sue Liu which is reproduced below.
 |
This triangle is a right angled isosceles triangle, the
hypotenuse being $\sqrt{2}b$. We draw a line through $A$ and point
$M$, the midpoint of the line $BC$. We draw the line $B`C`$ giving
another right angles isosceles triangle $AB`C`$, similar to
triangle $ABC$ but with sides a and hypotenuse $\sqrt{2}a$. Now $N$
is the point where the line $B`C`$ meets the line $AM$, and $P$ is
the point where $BC`$ meets $B`C$ (also on $AM$).
It is clear that triangle $PBC$ is similar to triangle $P
B`C`$ and the enlargement factor from $B`C`$ to $BC$ is $b/a$. So
the line $PM$ is $b/a$ times as long as the line $PN$. Also the
line $AN$ is half the length of $B`C`$, so it is $\sqrt{2}a/2$. The
line $AM$ is half the length of $BC$ so it is $\sqrt{2}b/2$.
|
If we let $PN$ be $x$ then we have an equation:
$$x + \frac{bx}{a} + \frac{\sqrt{2}}{2}a =
\frac{\sqrt{2}}{2}b$$
Solving this equation gives $$x =
{\frac{\sqrt{2}}{2}}{\frac{(b - a)a}{(a + b)}}$$
$PM$ is the height of the shaded triangle and $PM =
xb/a$.
Area of the shaded triangle is:
$$\frac{xb}{a} \cdot \frac{\sqrt{2}}{2} \cdot b =
\frac{b^{2}(b - a)}{2(b + a)}$$
You may also like
Golden Thoughts
Rectangle PQRS has X and Y on the edges. Triangles PQY, YRX and XSP have equal areas. Prove X and Y divide the sides of PQRS in the golden ratio.
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?
Contact
A circular plate rolls in contact with the sides of a rectangular tray. How much of its circumference comes into contact with the sides of the tray when it rolls around one circuit?