Skip over navigation
Congratulations Andrei Lazanu, age 14, School No.205, Bucharest, Romania on another beautiful solution.
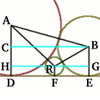
I denoted by $A$ the centre of the circle of radius $a/b$, by $B$ the centre of the radius $a$, by $C$ the circle of radius $b$, by $D$ the centre of the circle of radius $b/a$, by $E$ the centre of the circle of radius $1$/a, by $F$ the centre of the circle of radius $1/b$ and by $O$ the centre of the circle of radius 1.
I observed that the triangles obtained have the following sides:
I observe that triangles $BCO$, $DEO$ and $FAO$ are similar, with the similarity ratios (taking them two by two), $1: 1/a: 1/b$ respectively. So are triangles $ABO$, $CDO$ and $EFA$, with the similarity ratios $a: b: 1$.
Looking in the similarity ratio, I observe that angle $BOC$ is congruent with angle $DEO$ and with angle $AFO$, angle $OBC$ with angles $FAO$ and $EOD$, and angle $BCO$ with $ODE$ and $AOF$.
This means the sum of angles $BOC$, $AOF$ and $DOE$ is the angle sum in a triangle, i.e. $180^0$.
For triangles $AOB$, $COD$ and $EOF$ that are similar, angles $AOB$, $ODC$ and $OEF$ are congruent; so are angles $OAB$, $OFE$ and $DOC$ and $ABO$, $OCD$ and $FOE$. In this case the sum of angles: $AOB$, $COD$ and $EOF$ is $180^0$.
So, the sum of all angles around point O is $360^0$. This means that, with the given radii, it is always possible to construct such a flower.
Flower
Age 16 to 18
Challenge Level 
I denoted by $A$ the centre of the circle of radius $a/b$, by $B$ the centre of the radius $a$, by $C$ the circle of radius $b$, by $D$ the centre of the circle of radius $b/a$, by $E$ the centre of the circle of radius $1$/a, by $F$ the centre of the circle of radius $1/b$ and by $O$ the centre of the circle of radius 1.
I observed that the triangles obtained have the following sides:
| ABO | a/b + a | a +1 | a/b +1 |
| BCO | a + b | a + 1 | b + 1 |
| CDO | b + b/a | b + 1 | b/a + 1 |
| DEO | b/a + 1/a | b/a + 1 | 1/a + 1 |
| EFA | 1/a +1/b | 1 + 1/b | 1 + 1/a |
| FAO | a/b + 1/b | a/b + 1 | 1/b + 1 |
I observe that triangles $BCO$, $DEO$ and $FAO$ are similar, with the similarity ratios (taking them two by two), $1: 1/a: 1/b$ respectively. So are triangles $ABO$, $CDO$ and $EFA$, with the similarity ratios $a: b: 1$.
Looking in the similarity ratio, I observe that angle $BOC$ is congruent with angle $DEO$ and with angle $AFO$, angle $OBC$ with angles $FAO$ and $EOD$, and angle $BCO$ with $ODE$ and $AOF$.
This means the sum of angles $BOC$, $AOF$ and $DOE$ is the angle sum in a triangle, i.e. $180^0$.
For triangles $AOB$, $COD$ and $EOF$ that are similar, angles $AOB$, $ODC$ and $OEF$ are congruent; so are angles $OAB$, $OFE$ and $DOC$ and $ABO$, $OCD$ and $FOE$. In this case the sum of angles: $AOB$, $COD$ and $EOF$ is $180^0$.
So, the sum of all angles around point O is $360^0$. This means that, with the given radii, it is always possible to construct such a flower.
You may also like
Baby Circle
A small circle fits between two touching circles so that all three circles touch each other and have a common tangent? What is the exact radius of the smallest circle?
Fixing It
A and B are two fixed points on a circle and RS is a variable diamater. What is the locus of the intersection P of AR and BS?
Kissing
Two perpendicular lines are tangential to two identical circles that touch. What is the largest circle that can be placed in between the two lines and the two circles and how would you construct it?