Skip over navigation
Circle Scaling
Age 14 to 16
Challenge Level 
You are given a circle with centre O. Describe how to construct with a straight edge and a pair of compasses, two other circles centre O so that the three circles have areas in the ratio 1:2:3.
You may also like
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
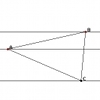
Pareq Exists
Prove that, given any three parallel lines, an equilateral triangle always exists with one vertex on each of the three lines.
The Medieval Octagon
Medieval stonemasons used a method to construct octagons using ruler and compasses... Is the octagon regular? Proof please.