Up and Down Staircases
Up and Down Staircases
One block is needed to make an up-and-down staircase, with one step up and one step down.
Four blocks make an up-and-down staircase with two steps up and two steps down.
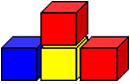
How many blocks would be needed to build an up-and-down staircase with three steps up and three steps down?
What about for four steps up and four steps down?
What do you notice about the number of blocks needed each time?
Can you predict how many blocks will be needed to build an up-and-down staircase with five steps up and five steps down?
Were you right?
Explain how you would work out the number of blocks needed to build a staircase with any number of steps.
Why do this problem?
Possible approach
You could introduce this problem by building the staircases with one and two steps respectively. Explain how each is named and ask how many blocks are needed to build each. You could invite some learners to explain how they counted the total number of cubes in each case.
Ask the children to close their eyes and imagine the next staircase, which would have three steps up and three steps down. Can they picture in their heads (visualise) the number of blocks needed in total? Ask a few learners to explain how they were picturing the staircase and how they knew the total number of blocks.
Suggest that you'd like to know how many blocks would be needed to build a much bigger staircase, for example twenty steps up and twenty down. Invite pupils to suggest how they might answer this question if they didn't have enough cubes. Some may say to draw it, but you could protest that this would take too long! Encourage them to look carefully at the numbers they have found so far, perhaps by drawing a table on the board:
| Number of steps up | Total number of blocks |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
Children do not necessarily need to know about squaring numbers in order to express the relationship, it can be explained in terms of 'multiplying a number by itself'. You may find they need to create more staircases before being able to generalise fully.
As a final challenge, ask them if they can see why square numbers are produced. You may like to show the picture in the Getting Started section, or use cubes to show the same thing. This is an ideal opportunity to emphasise that square numbers are called square numbers precisely because that
number of, for example, dots can be arranged in a square array.
Once the relationship is articulated, children will enjoy working out the number of cubes needed for huge staircases!
Key questions
Can you predict the number of cubes in the next staircase? How did you know?
Do you notice any patterns in the number of steps compared with the total number of cubes?
How could you record your results for each staircase?
Possible support
You could supply some children with a table ready to be filled in.
Possible extension
This document gives details of two possible extension ideas. Children could explore the numbers of cubes in each 'column' of the staircases, or investigate other kinds of staircases.
You may also like
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?
Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?
Sweets in a Box
How many different shaped boxes can you design for 36 sweets in one layer? Can you arrange the sweets so that no sweets of the same colour are next to each other in any direction?