Squirty

Thanks to Andrei of School 205 Bucharest for this well explained solution.

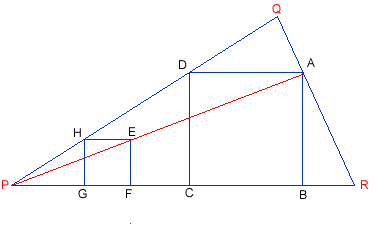
• First, I drew a line $HG$, perpendicular on $P$, and a line through H, parallel with $PR$.
• On it, I took a segment $HE$ of the same length with $HO$.
• Then I finished drawing the square $HEFO$, drawing $EF$ perpendicular on $PR$. The line PE intersects $QR$ in $A$.
• From $A$ I drew a parallel to $PR$ (let the intersection point with $PQ$ be $D$), and a perpendicular to $PR$ (let the intersection point with $PR$ be $B$).
• This way I found 3 vertices of the rectangle $ABCD$, and I finished the rectangle finding the vertex $C$ on $PR$, so that $CD$ is perpendicular to $PR$.

The rectangle $ABCD$ is a square because:- Triangles $PEF$ and $PAB$ are similar, they are both right-angled triangles, with a common angle. The similarity ratio is: $${{PE}\over{PA}} = {{EF} \over {AB}}$$ Triangles $PEH$ and $PAD$ are similar, because angles $PEH$ and $PAD$ are equal and $HPE$ is a common angle. The similarity ratio $$\frac{PE}{PA} = \frac{HE}{AD}$$ From $(1)$ and $(2)$ $$ \frac{AB}{EF} = \frac{AD}{HE}$$ As $HE=EF$ (sides of a square) Therefore $ AB =AD$ $ ABCD$ is a rectangle with two adjacent sides equal

Therefore $ ABCD$ is a square.

Now, the construction of the inscribed square must be done in the following steps:

• Choose a point $H$ on side $PQ$, near $P$
• Draw line $HG$, perpendicular on $PR$
• Take the distance $HG$ as the compass distance, and draw a circle arc, with centre $G$. $F$ is the point of intersection of this arc with $PR$.
• Construct two circle arcs with centres $F$ and $H$ (with the same radius as before). Their intersection is point $E$, and $EFGH$ is a square.
• Draw line $PE$. Let the intersection point of this line with side $QR$ be $A$.
• Draw from $A$ parallel to $EF$ and $HE$. Their intersections with $PR$ and $QP$ are points $B$ and $D$ respectively.
• Draw from $D$ a parallel to $AB$. Its intersection with $PR$ is $C$.
• $ABCD$ is the square to be found.