Seven Squares - Group-worthy Task

Three students were asked to draw this matchstick pattern:

This is how Phoebe drew it:

Can you describe what Phoebe did?

How many 'downs' and how many inverted C's are there?
How many matchsticks altogether?

Now picture what Phoebe would do if there had been $25$ squares.
How many 'downs' and how many inverted C's would there be?
How many matchsticks altogether?

If there had been $100$ squares? How many matchsticks altogether?
A million and one squares? How many matchsticks?

This is how Alice drew it:

Can you describe what Alice did?

How many 'alongs' and how many 'downs' are there?
How many matchsticks altogether?

Now picture what Alice would do if there had been $25$ squares.
How many 'alongs' and how many 'downs' would there be?
How many matchsticks altogether?

If there had been $100$ squares? How many matchsticks altogether?
A million and one squares? How many matchsticks?

This is how Luke drew it:

Can you describe what Luke did?

How many squares and how many inverted C's are there?
How many matchsticks altogether?

Now picture what Luke would do if there had been $25$ squares.
How many squares and how many inverted C's would there be?
How many matchsticks altogether?

If there had been $100$ squares? How many matchsticks altogether?
A million and one squares? How many matchsticks?
 

Now choose a couple of the sequences below.

Try to picture how to make the next, and the next, and the next...

Use this to help you find the number of squares, or lines, or perimeter, or dots needed for the $25^{th}$, $100^{th}$ and $n^{th}$ pattern.

Can you describe your reasoning?

Growing rectangles

This rectangle has height 2 and width 3.

Work out the perimeter, the number of dots, and the number of lines needed to draw a rectangle with:

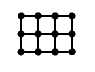
• height 2 and width 25
• height 2 and width 100
• height 2 and width n

L shapes

This L shape has height 4 and width 4.

Work out the perimeter, the number of squares, and the number of lines needed to draw an L shape with:

 

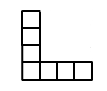
• height 25 and width 25
• height 100 and width 100
• height n and width n

Two squares

This pattern with two squares has four black dots.

Work out the number of white dots and the number of lines needed to draw a pattern with:

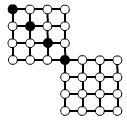
• 25 black dots
• 100 black dots
• n black dots

Square of Squares

This pattern has side length 5.

Work out the number of edge squares and the number of lines needed to draw the pattern with:

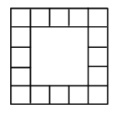
• side length 25
• side length 100
• side length n

Dots and More Dots

This pattern has side length 3.

Work out the number of dots and the number of lines needed to draw the pattern with:

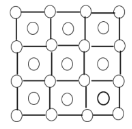
• side length 25
• side length 100
• side length n

Rectangle of Dots

This pattern is made from two joined squares with side length 3.

 

 

Work out the number of lines and the number of dots needed to draw the pattern of joined squares with:

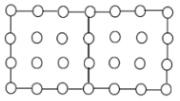
• side length 25
• side length 100
• side length n