Changing Places

A four by four square grid contains fifteen counters with the bottom left hand square empty. The counter in the top right hand square is red and the rest are blue. The aim is to slide the red counter from its starting position to the bottom left hand corner in the least number of moves. You may only slide a counter into an empty square by moving it up, down, left or right but not diagonally.
 

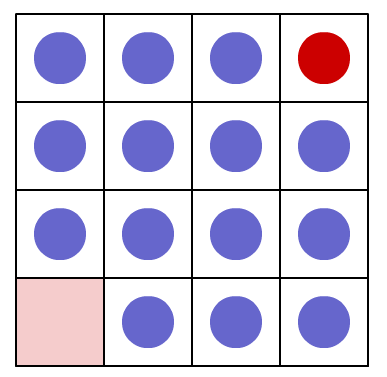
Explore a four by four array. How many moves did you take to move the red counter to HOME (pink square)?

Can you do it in fewer moves? What is the least number of moves you can do it in?

Try a smaller array. How many moves did you take to move the red counter to HOME?
Try a larger array. What is the least number of moves you can do it in?

Have you a strategy for moving down each array?

On which move does the red counter make its first move?

On which moves does the red counter make its other moves?
Can you predict the number of moves that the red counter makes on the way HOME?
Why is the least number of moves ALWAYS odd?
Can you predict what the least number of moves will be for any square array?

Can you explain why YOUR rule works?

You can take this further by considering similar ideas using rectangular arrays or in three dimensions.