Hamilton's Puzzle

Age 7 to 11

Challenge Level Yellow star

Hamilton's Puzzle

In 1859, the Irish mathematician Sir William Rowan Hamilton devised a puzzle with a regular dodecahedron made of wood. Here is a dodecahedron:

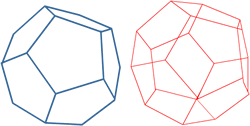
He labelled each of the vertices with the name of an important city. The challenge was to find a route along the edges of the dodecahedron which visited every city exactly once and returned to the start.

Here is a graph which represents the dodecahedron. Can you see how each of the 20 vertices, 30 edges and 12 pentagonal faces is represented in the graph?

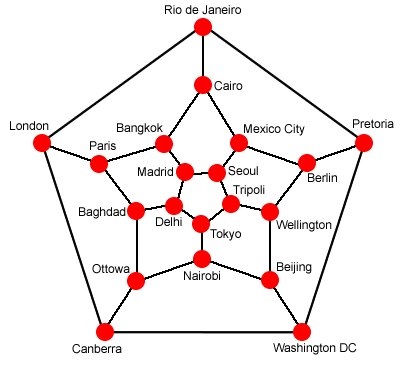
I start my journey in Rio de Janeiro and visit all the cities as Hamilton described, passing through Canberra before Madrid, and then returning to Rio. What route could I have taken?

Can you find any other ways of making this journey?

Here is a simpler network of countries:

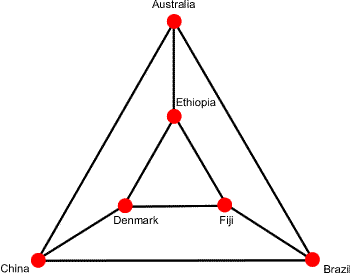
How many different ways are there of visiting each of these countries once and only once, beginning and ending at Australia?

Why do this problem?

Possible approach

There are many possible routes in the first part of this problem and finding all of them in a systematic way is perhaps too challenging at this level. Asking the pupils to look for several different paths will hopefully help them realise just how many possibilities there are without the need to find an exhaustive list.

Key questions

Possible extension

Pupils may like to make their own Hamiltonian puzzle, labelling each vertex with the name of a city. They could then write a list of the cities in the order you would have to go to visit each once and only once, and challenge a friend to find the route.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Hamilton's Puzzle