Skip over navigation
We received three good solutions - two almost completely correct, fromYanqing from Lipson Community College and from Sarah from Colyton, and one completely correct from Andrei from Tudor Vianu College in Bucharest. Well done to you all.
Andrei's solution follows:
First, I observe that for the first figure it is impossible to cross each bridge once. This happens because you would remain in a place where all the bridges were already crossed.
In the second case, it is possible to cross the bridges only once and create a circuit.
I worked with different number of bridges and islands and I obtained solutions for each of the following:
- bridge traversing circuits
- bridge traversing paths
- Hamiltonian circuits
- Situations where none of the above is possible.
For 8 bridges I found:
- A diagram with a bridge traversing circuit.
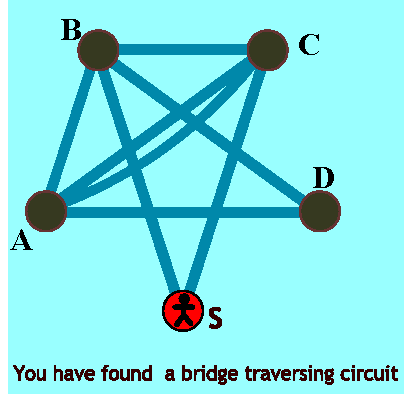
The circuit is the following: S-C-A-D-B-A-C-B-S
- A diagram with a bridge traversing path:
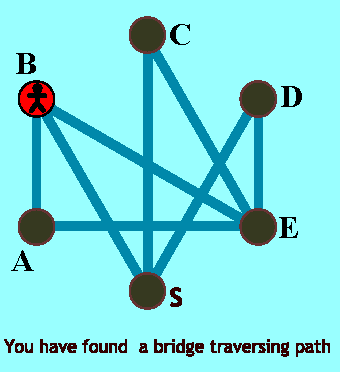
The path is the following: S-D-E-A-B-S-C-E-B.
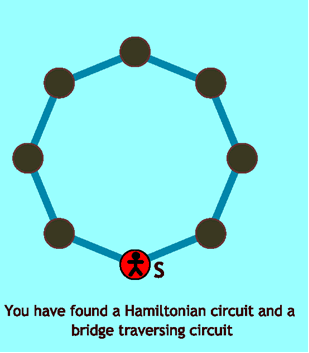
- A Hamiltonian circuit and a bridge traversing circuit:
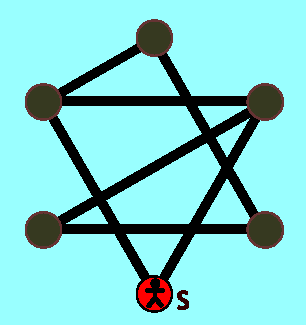
- A diagram in which neither is possible. In the diagram below, neither a traversing path nor a traversing circuit is possible:
Editor's note:
If you were allowed to start at another island you could have a traversable path: starting at the top right hand island and finishing in the top left hand island, or vice versa.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
The Bridges of Konigsberg
Age 11 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We received three good solutions - two almost completely correct, fromYanqing from Lipson Community College and from Sarah from Colyton, and one completely correct from Andrei from Tudor Vianu College in Bucharest. Well done to you all.
Andrei's solution follows:
First, I observe that for the first figure it is impossible to cross each bridge once. This happens because you would remain in a place where all the bridges were already crossed.
In the second case, it is possible to cross the bridges only once and create a circuit.
I worked with different number of bridges and islands and I obtained solutions for each of the following:
- bridge traversing circuits
- bridge traversing paths
- Hamiltonian circuits
- Situations where none of the above is possible.
For 8 bridges I found:
- A diagram with a bridge traversing circuit.

The circuit is the following: S-C-A-D-B-A-C-B-S
- A diagram with a bridge traversing path:

The path is the following: S-D-E-A-B-S-C-E-B.
- A Hamiltonian circuit and a bridge traversing circuit:

- A diagram in which neither is possible. In the diagram below, neither a traversing path nor a traversing circuit is possible:

Editor's note:
If you were allowed to start at another island you could have a traversable path: starting at the top right hand island and finishing in the top left hand island, or vice versa.
You may also like
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!
Fixing It
A and B are two fixed points on a circle and RS is a variable diamater. What is the locus of the intersection P of AR and BS?

