Skip over navigation

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Building Blocks
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Building Blocks
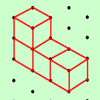
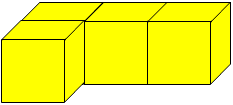
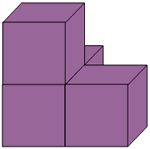
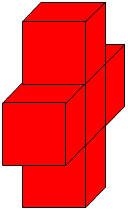
Here are some pictures of 3D shapes made from cubes. Can you make these shapes yourself?
What do they look like from different positions? Please send us photographs or pictures of your models.
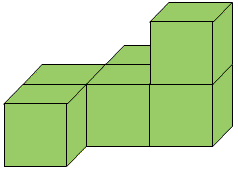
Why do this problem?
Working from 2D representations to 3D can be quite problematic at this level, and this problem gives children experience of doing just that, as well as then possibly transferring back to 2D. The activity provides a great opportunity to develop children's familiarity with positional language, for example behind,
in front, to the left, to the right, above/on top, below/underneath etc.
Possible approach
For this activity, you'll need plenty of multilink cubes. Display the picture on the screen of the interactive whiteboard, or project it onto an ordinary board. You could start with one of the shapes, for example the yellow one, and ask children to describe it. Encourage them to talk about the number of cubes used and their relative positions. Some learners might say it looks like an 'L'
shape.
Ask children to make the yellow shape, individually or in pairs, and they can compare the shapes to check they're the same. Depending on your class' experiences, you could then challenge them to draw their shape on isometric paper , sketch their shape on plain paper, or just put their shape on the table in
front of them so that it looks different from the picture in the problem.
The other shapes could be tackled in similar ways and you could take some photographs of the results for display alongside a print-out of the problem itself.
Key questions
How many cubes will you need for that shape?
Can you describe how they are joined together?
Possible extension
Some pupils might like to try The Third Dimension problem which is much more challenging and requires drawing on isometric paper.
Possible support
It may be useful to have each of the shapes made up yourself prior to the lesson so that you could show them to the group. Children are likely to find it easier to replicate a shape if they can see a 'real' version rather than just a picture.
You may also like
New House
In this investigation, you must try to make houses using cubes. If the base must not spill over 4 squares and you have 7 cubes which stand for 7 rooms, what different designs can you come up with?
The Third Dimension
Here are four cubes joined together. How many other arrangements of four cubes can you find? Can you draw them on dotty paper?

