Skip over navigation
Here to There 1 2 3
Age 5 to 7
Challenge Level 
Here to There 1 2 3
Move from the START to the FINISH by moving across, down or up to the next square. You can only move into each square once.
Add the numbers as you go.
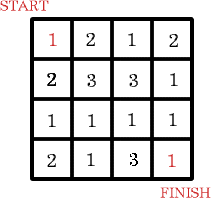
Find the path that gives the smallest total.
Find the path that gives the highest total.
Find a path that equals exactly 12.
How many paths make 12?
Why do this problem?
This activity can be fun to do and the pupils will be doing a number of calculations - probably without them realising it. It has the facility to be extended very easily. This problem provides children with the opportunity to make sense of numbers and reason about them. Systematic working is also involved.Possible approach
Key questions
How did you decide on your route?
Possible extension
Ask the pupils to invent new ones and ask them how they make them harder/easier.
Possible support
Some templates of the 4 by 4 square could be useful.
You may also like
Homes
Six new homes are being built! They can be detached, semi-detached or terraced houses. How many different combinations of these can you find?
Number Squares
Start with four numbers at the corners of a square and put the total of two corners in the middle of that side. Keep going... Can you estimate what the size of the last four numbers will be?
