Skip over navigation
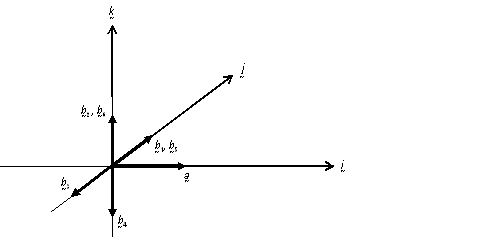

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
V-P Cycles
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Derek Wan gave an excellent solution and we include his
diagram of the final result at the end. Here's a solution from
Thomas Lauffenberger who finally reveals that he is an
American.
Suppose the vector product ${\bf a} \times {\bf b}\neq {\bf
0}$. Define a sequence of vectors ${\bf b_0},\ {\bf b_1},\ {\bf
b_2}\ldots $ by ${\bf b_0}={\bf b}$ and ${\bf b_{n+1}}={\bf
a}\times {\bf b_n}$
Part 1:
Show that ${\bf b_n} \rightarrow 0$ as $n \rightarrow \infty$
if ${\bf |a|} < 1$. \par According to the article supplied on
the basics of vector multiplication, the resulting vector is
perpendicular to its parents and has a magnitude of ${\bf
|v_1||v_2|} \sin \theta$. In the problem posed, we are given that
${\bf |a|}$ is less than 1. The maximum value of $\sin \theta$ is
1, so the product ${\bf |a|}\sin \theta$ must be less than 1; the
magnitudes of the succeeding vectors in the sequence given by ${\bf
b_{n+1}}={\bf a}\times {\bf b_n}$ decrease as a geometric series,
so they will tend to 0 as $n$ tends to infinity. The only vector
with a magnitude off 0 is the zero vector, which ${\bf b_n}$ will
tend to as $n$ tends to infinity.
Part 2:
Here $|{\bf a}|=1$ and $|{\bf b_1}|=r$. The supplied hint
suggests using ${\bf a} = {\bf i}$ and ${\bf b_1}= r{\bf j}$. Doing
the cross product matrix math (a $3 \times 3$ matrix with "${\bf
i}, {\bf j}, {\bf k}$" on the top line, "$1,0,0$" for the ${\bf a}$
line, and "$0,r,0$" for ${\bf b_1}$, we obtain ${\bf b_2}= r{\bf
k}$. Performing the next cross product, ${\bf a} \times {\bf b_2}$,
we obtain $-r{\bf j}$, and, doing it again, $-r{\bf k}$. The cross
product ${\bf a}\times {\bf b_4}$ produces a result of $r{\bf j}$
which is ${\bf b_1}$; therefore, we have a cycle.
If we begin our movement from the origin in 3-space, ${\bf
b_1}$ tells us to advance $r$ units up the $y$-axis ${\bf j}$
direction). Then ${\bf b_2}$ says to advance $r$ units positively
along the $z$-axis. Vectors ${\bf b_3}$ and ${\bf b_4}$,
respectively, move again along the $y$ and $z$ axes, but now $r$
units in the negative direction. The shape that follows is a square
with sides of $r$ units, located within the $yz$-plane in this
instance. I'm sure that much more can be said about this, regarding
our choices for ${\bf a}$ and ${\bf b}$; I'll do more work on it
and post back more ideas. \par Addendum to previous submission- The
key components determining the location of the square are ${\bf
a}$, a unit vector, and $\bf {b}$, a vector of magnitude $r$.
Vector ${\bf a}$ determines the plane in which the square will
situate itself which has vector ${\bf a}$ perpendicular to the
plane of the square; ${\bf b}$ moves within that plane. With the
direction vector ${\bf a}$ pointed up relative to our perspective,
the motion of the vector ${\bf b}$ is to trace the square in a
counterclockwise direction, like a baseball diamond. (Yes, I'm an
American!)
Thomas is adding one vector onto the previous one to generate
a square. Here is Derek Wan's sketch of all 6 vectors:
We can see that the vectors lie on the $y$-$z$ plane
perpendicular to the vector ${\bf a}$.
You may also like
Flexi Quads
A quadrilateral changes shape with the edge lengths constant. Show the scalar product of the diagonals is constant. If the diagonals are perpendicular in one position are they always perpendicular?
A Knight's Journey
This article looks at knight's moves on a chess board and introduces you to the idea of vectors and vector addition.
8 Methods for Three by One
This problem in geometry has been solved in no less than EIGHT ways by a pair of students. How would you solve it? How many of their solutions can you follow? How are they the same or different? Which do you like best?

