Skip over navigation
Vectors - What Are They? gives an introduction to the subject.
There are two useful definitions of multiplication of vectors, in one the product is a scalar and in the other the product is a vector. There is no operation of division of vectors. In some school syllabuses you will meet scalar products but not vector products but we discuss both types of multiplication of vectors in this article to give a more rounded picture of the basics of the subject
The scalar product of vectors ${\bf u} = (u_1, u_2, u_3)$ and ${\bf v}=(v_1, v_2, v_3)$ is a scalar defined to be $${\bf u.v}= u_1v_1 + u_2v_2 + u_3v_3\quad (1).$$ This is sometimes called the inner product or dot product . It follows immediately from the definition that $${\bf u.u} = u_1^2+u_2^2+u_3^2=|{\bf u}|^2 \quad (2),$$ and if ${\bf i, j, k}$ are unit vectors along the axes then $${\bf i.i}={\bf j.j} = {\bf k.k} = 1,\quad {\rm and}\quad {\bf i.j}={\bf j.k} = {\bf k.i} = 0\quad (3).$$ It is left to the reader to check from the definition that $${\bf u.v} = {\bf v.u}, \ {\rm and} \ ({\bf u + v}).{\bf w} = {\bf u.w}+{\bf v.w}.$$ This shows that we can expand or multiply out $${\bf u.v}= (u_1{\bf i}+u_2{\bf j}+u_3{\bf k}).(v_1{\bf i}+v_2{\bf j}+u_3{\bf k})$$ giving nine terms. Using equation (3) six of these terms are zero and the other three give the expression $u_1v_1+u_2v_2+u_3v_3$ consistent with the definition in equation (1).
The Cosine Rule in Euclidean Geometry can be proved without the use of scalar products. Using the Cosine Rule for the triangle $\Delta OPQ$ where $\angle POQ = \theta$ we get: $$|{\bf u-v}|^2 =|{\bf u}|^2 + |{\bf v}|^2 - 2|{\bf u}||{\bf v}|\cos \theta.\quad (4) $$
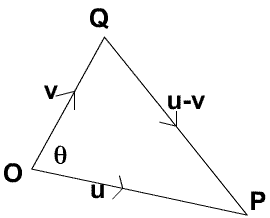
Expanding $|{\bf u-v}|^2$ we get $$|{\bf u-v}|^2 = ({\bf u}-{\bf v}).({\bf u}-{\bf v})= |{\bf u}|^2 + |{\bf v}|^2 - 2{\bf u}.{\bf v},\quad (5).$$ Hence, from equations (4) and (5), we get the very useful result $${\bf u.v} = |{\bf u}||{\bf v}|\cos \theta, \quad (6)$$ where angle $\theta$ is the angle between the vectors ${\bf u}$ and ${\bf v}$. This is a very important and useful result because it enables us to find the angle between two vectors.
Some texts use the formula (6) to define the angle between two vectors, that is $$\theta = \cos^{-1} \left({{\bf u.v}\over |{\bf u}|||{\bf v}|}\right)\quad (7).$$ In three dimensions we can use a more intuitive definition of angle in terms of turning, but in higher dimensions it is necessary to have a definition of angle such as formula (7). If we use this formula to define an angle then the Cosine Rule follows directly as the two are equivalent.
Note that the product of a row vector and a column vector is defined in terms of the scalar product and this is consistent with matrix multiplication. $$(u_1\ u_2\ u_3)\left( \begin{array}{cc} v_1 \\ v_2 \\ v_3 \end{array} \right) = u_1v_1 + u_2v_2 + u_3v_3.$$
The vector product of two vectors ${\bf b}$ and ${\bf c}$, written ${\bf b}\times {\bf c}$ (and sometimes called the cross product ), is the vector $${\bf b}\times {\bf c} = \left( \begin{array}{cc} b_2c_3-b_3c_2 \\ b_3c_1 -b_1c_3 \\ b_1c_2 -b_2c_1 \end{array} \right) \quad (8).$$ There is an alternative definition of the vector product, namely that ${\bf b}\times {\bf c}$ is a vector of magnitude $|{\bf b}||{\bf c}|\sin \theta$ perpendicular to ${\bf b}$ and ${\bf c}$ and obeying the 'right hand rule', and we shall prove that this result follows from the given definition and that the two definitions are equivalent. The proof is given later for completeness but first we consider ${\bf b}\times {\bf c}$ expressed in terms of components in the directions of ${\bf i, j, k}$.
From this definition we can see that ${\bf b}\times {\bf c}=-{\bf c}\times {\bf b}$ so this operation is not commutative. If ${\bf i, j, k}$ are unit vectors along the axes then, from this definition: $${\bf i}\times {\bf i} = {\bf j}\times {\bf j}= {\bf k}\times {\bf k},$$ and $$\eqalign{ {\bf i}\times {\bf j} &= {\bf k},\quad {\bf j}\times {\bf i} = -{\bf k} \cr {\bf j}\times {\bf k} &= {\bf i},\quad {\bf k}\times {\bf j} = -{\bf i} \cr{\bf k}\times {\bf i} &= {\bf j},\quad {\bf i}\times {\bf k} = -{\bf j} .}$$ From the definition it follows that $$k({\bf b}\times {\bf c}) = (k{\bf b})\times {\bf c} = {\bf b} \times (k{\bf c}), \quad\quad ({\bf a+b})\times {\bf c} = ({\bf a}\times {\bf c}) + ({\bf b}\times {\bf c}).$$ Expanding the expression $${\bf b}\times {\bf c} = (b_1{\bf i} + b_2{\bf j} + b_3 {\bf k}) \times (c_1{\bf i}+ c_2{\bf j} + c_3 {\bf k})$$ gives $$ (b_2c_3-b_3c_2){\bf i}+ (b_3c_1-b_1c_3){\bf j} + (b_1c_2-b_2c_1){\bf k} \quad (9)$$ which is the formula for the vector product given in equation (8).
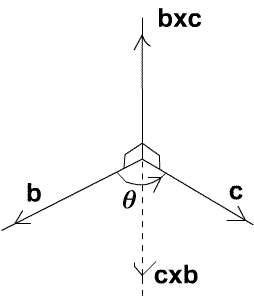
Now we prove that the two definitions of vector multiplication are equivalent. The diagram shows the directions of the vectors ${\bf b}$, ${\bf c}$ and ${\bf b}\times {\bf c}$ which form a 'right handed set'.
Multiplication of Vectors
Vectors - What Are They? gives an introduction to the subject.
There are two useful definitions of multiplication of vectors, in one the product is a scalar and in the other the product is a vector. There is no operation of division of vectors. In some school syllabuses you will meet scalar products but not vector products but we discuss both types of multiplication of vectors in this article to give a more rounded picture of the basics of the subject
Scalar Multiplication
The scalar product of vectors ${\bf u} = (u_1, u_2, u_3)$ and ${\bf v}=(v_1, v_2, v_3)$ is a scalar defined to be $${\bf u.v}= u_1v_1 + u_2v_2 + u_3v_3\quad (1).$$ This is sometimes called the inner product or dot product . It follows immediately from the definition that $${\bf u.u} = u_1^2+u_2^2+u_3^2=|{\bf u}|^2 \quad (2),$$ and if ${\bf i, j, k}$ are unit vectors along the axes then $${\bf i.i}={\bf j.j} = {\bf k.k} = 1,\quad {\rm and}\quad {\bf i.j}={\bf j.k} = {\bf k.i} = 0\quad (3).$$ It is left to the reader to check from the definition that $${\bf u.v} = {\bf v.u}, \ {\rm and} \ ({\bf u + v}).{\bf w} = {\bf u.w}+{\bf v.w}.$$ This shows that we can expand or multiply out $${\bf u.v}= (u_1{\bf i}+u_2{\bf j}+u_3{\bf k}).(v_1{\bf i}+v_2{\bf j}+u_3{\bf k})$$ giving nine terms. Using equation (3) six of these terms are zero and the other three give the expression $u_1v_1+u_2v_2+u_3v_3$ consistent with the definition in equation (1).
The Cosine Rule in Euclidean Geometry can be proved without the use of scalar products. Using the Cosine Rule for the triangle $\Delta OPQ$ where $\angle POQ = \theta$ we get: $$|{\bf u-v}|^2 =|{\bf u}|^2 + |{\bf v}|^2 - 2|{\bf u}||{\bf v}|\cos \theta.\quad (4) $$
Expanding $|{\bf u-v}|^2$ we get $$|{\bf u-v}|^2 = ({\bf u}-{\bf v}).({\bf u}-{\bf v})= |{\bf u}|^2 + |{\bf v}|^2 - 2{\bf u}.{\bf v},\quad (5).$$ Hence, from equations (4) and (5), we get the very useful result $${\bf u.v} = |{\bf u}||{\bf v}|\cos \theta, \quad (6)$$ where angle $\theta$ is the angle between the vectors ${\bf u}$ and ${\bf v}$. This is a very important and useful result because it enables us to find the angle between two vectors.
Some texts use the formula (6) to define the angle between two vectors, that is $$\theta = \cos^{-1} \left({{\bf u.v}\over |{\bf u}|||{\bf v}|}\right)\quad (7).$$ In three dimensions we can use a more intuitive definition of angle in terms of turning, but in higher dimensions it is necessary to have a definition of angle such as formula (7). If we use this formula to define an angle then the Cosine Rule follows directly as the two are equivalent.
Note that the product of a row vector and a column vector is defined in terms of the scalar product and this is consistent with matrix multiplication. $$(u_1\ u_2\ u_3)\left( \begin{array}{cc} v_1 \\ v_2 \\ v_3 \end{array} \right) = u_1v_1 + u_2v_2 + u_3v_3.$$
Vector Multiplication
The vector product of two vectors ${\bf b}$ and ${\bf c}$, written ${\bf b}\times {\bf c}$ (and sometimes called the cross product ), is the vector $${\bf b}\times {\bf c} = \left( \begin{array}{cc} b_2c_3-b_3c_2 \\ b_3c_1 -b_1c_3 \\ b_1c_2 -b_2c_1 \end{array} \right) \quad (8).$$ There is an alternative definition of the vector product, namely that ${\bf b}\times {\bf c}$ is a vector of magnitude $|{\bf b}||{\bf c}|\sin \theta$ perpendicular to ${\bf b}$ and ${\bf c}$ and obeying the 'right hand rule', and we shall prove that this result follows from the given definition and that the two definitions are equivalent. The proof is given later for completeness but first we consider ${\bf b}\times {\bf c}$ expressed in terms of components in the directions of ${\bf i, j, k}$.
From this definition we can see that ${\bf b}\times {\bf c}=-{\bf c}\times {\bf b}$ so this operation is not commutative. If ${\bf i, j, k}$ are unit vectors along the axes then, from this definition: $${\bf i}\times {\bf i} = {\bf j}\times {\bf j}= {\bf k}\times {\bf k},$$ and $$\eqalign{ {\bf i}\times {\bf j} &= {\bf k},\quad {\bf j}\times {\bf i} = -{\bf k} \cr {\bf j}\times {\bf k} &= {\bf i},\quad {\bf k}\times {\bf j} = -{\bf i} \cr{\bf k}\times {\bf i} &= {\bf j},\quad {\bf i}\times {\bf k} = -{\bf j} .}$$ From the definition it follows that $$k({\bf b}\times {\bf c}) = (k{\bf b})\times {\bf c} = {\bf b} \times (k{\bf c}), \quad\quad ({\bf a+b})\times {\bf c} = ({\bf a}\times {\bf c}) + ({\bf b}\times {\bf c}).$$ Expanding the expression $${\bf b}\times {\bf c} = (b_1{\bf i} + b_2{\bf j} + b_3 {\bf k}) \times (c_1{\bf i}+ c_2{\bf j} + c_3 {\bf k})$$ gives $$ (b_2c_3-b_3c_2){\bf i}+ (b_3c_1-b_1c_3){\bf j} + (b_1c_2-b_2c_1){\bf k} \quad (9)$$ which is the formula for the vector product given in equation (8).
Now we prove that the two definitions of vector multiplication are equivalent. The diagram shows the directions of the vectors ${\bf b}$, ${\bf c}$ and ${\bf b}\times {\bf c}$ which form a 'right handed set'.
You may wish to finish reading here and it is indeed more
important to appreciate that there are two definitions of a vector
product, which can be shown to be equivalent, than it is
mechanically to work through the details of the proof.
Theorem The vector
product of two vectors ${\bf b}$ and ${\bf c}$ is a vector ${\bf
b}\times {\bf c}$ with the following properties:
(i) ${\bf b}\times {\bf c}$ has
magnitude $|{\bf b}||{\bf c}|\sin \theta$ where $\theta$ is the
angle between the directions of ${\bf b}$ and ${\bf c}$;
(ii) ${\bf b}\times {\bf c}$ is
perpendicular to ${\bf b}$ and ${\bf c}$ with direction such that
the vectors ${\bf b}$, ${\bf c}$ and ${\bf b}\times {\bf c}$ form a
right handed set as in the diagram so that ${\bf b}\times {\bf c}$
and ${\bf c}\times {\bf b}$ are in opposite directions.
Proof of part (i)
Consider the area of the parallelogram with sides given by the
vectors ${\bf b}$ and ${\bf c}$ and angle $\theta$ between these
sides. The area of this parallelogram is $|{\bf b}||{\bf c}|\sin
\theta$. The vector ${\bf b}$ can be decomposed into a vector
$k{\bf c}$ of magnitude $|{\bf b}|\cos \theta$ in the direction of
${\bf c}$ and ${\bf b}-k{\bf c}$ of magnitude $|{\bf b}|\sin
\theta$ perpendicular to ${\bf c}$ where $k=|{\bf b}|\cos
\theta/|{\bf c}|=({\bf b.c})/|{\bf c}|^2$.
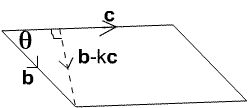
So the area of the parallelogram is: $$\eqalign{ |{\bf
c}||{\bf b}|\sin \theta &= |{\bf c}||{\bf b}-k{\bf c}| \cr
&= ||{\bf c}|{\bf b} - ({\bf b.c}){\bf c}/|{\bf c}||}$$ In
order to work out the modulus on the right hand side we take the
scalar product of the vector with itself. $$\eqalign{ |{\bf
c}||{\bf b}|\sin \theta &= (|{\bf c}|{\bf b} - ({\bf b.c}){\bf
c}/|{\bf c}|).(|{\bf c}|{\bf b} - ({\bf b.c}){\bf c}/|{\bf c}|) \cr
&= ({\bf b.b})|{\bf c}|^2 - 2({\bf b.c})^2 + ({\bf b.c})^2{\bf
c.c}/|{\bf c}|^2 \cr &=\sqrt{|{\bf b}|^2|{\bf c}|^2 - ({\bf
b.c})^2}\cr &=\sqrt{b_1^2+b_2^2+b_3^2
(c_1^2+c_2^2+c_3^2)-(b_1c_1+b_2c_2+b_3c_3)^2} \cr
&=\sqrt{(b_2c_3-b_3c_2)^2+(b_3c_1-b_1c_3)^2+(b_1c_2-b_2c_1)^2}
\cr &= |{\bf b}\times {\bf c}|. }$$
Proof of part (ii) To
show that ${\bf b}$ and ${\bf b}\times {\bf c}$ are perpendicular
we show that the scalar product is zero: $${\bf b}.{\bf b}\times
{\bf c} = b_1(b_2c_3-b_3c_2) +b_2(b_3c_1-b_1c_3)+b_3(b_1c_2-b_2c_1)
= 0,$$ and similarly the scalar product of ${\bf c}$ and ${\bf
b}\times {\bf c}$ is zero so these vectors are perpendicular.
Related Collections
You may also like
Flexi Quads
A quadrilateral changes shape with the edge lengths constant. Show the scalar product of the diagonals is constant. If the diagonals are perpendicular in one position are they always perpendicular?
A Knight's Journey
This article looks at knight's moves on a chess board and introduces you to the idea of vectors and vector addition.
8 Methods for Three by One
This problem in geometry has been solved in no less than EIGHT ways by a pair of students. How would you solve it? How many of their solutions can you follow? How are they the same or different? Which do you like best?