Dice, Routes and Pathways

So much of our work in shape and space in primary schools involves focusing on conveying a lot of information about the properties of geometric shapes, especially triangles and quadrilaterals that have specific regularities. What else is there to geometry and thinking about geometric ideas? In 2001 I was lucky enough to pay an extended visit to the Czech Republic and work in the Faculty of Education in Charles University in Prague. There I met Milan Trch and became interested in his ideas for developing what he calls "non-traditional" mathematical tasks or "non-standard problems".

Milan's concern is that in schools we tend to focus on textbook tasks that can be solved by most children using methods that are prescribed by the teacher. I think that this is true in British schools as much as in Czech schools. He set out to devise some geometric tasks in which the student does not know the solving method but can discover it for him/herself or in which he/she knows the method but does not realise that it is suitable for the new problem. At NRICH, these are just the kind of problems that we are interested in and write for the website.

Looking at Milan's ideas for problems, and arenas in which problems could be devised, I was struck by the richness of the scenarios that he had chosen and also the quality of mathematical thinking that some simple contexts were capable of provoking. Milan stresses his desire to devise problems that will motivate children and engage them as well as extend their mathematical thinking and develop their imaginations. The idea is to present settings in which there is no obvious method but in which children can be encouraged to think deeply about the context and extend their ability to think mathematically, especially geometrically. So what do these scenarios look like? The list is extensive and I do not have the space in this article to show you all Milan's ideas but here are a few to give you a taster.

Dice games

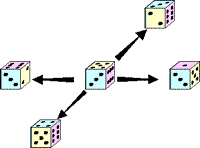Milan suggests placing a die on a square grid and recording the top number. The die is then turned onto one of the other faces. Then the top number is recorded again. We developed this idea into a game called Roll the Dice. The children we have used the activity with, are fascinated by the idea and, as well as asking for reasoning and justification, the task helps to develop recording skills and systematic approaches to possibilities. I think we are possibly getting better at encouraging these kinds of thinking in the context of number work but in shape and space we do tend to be prescriptive. This problem offers us a geometric context in which to develop mathematical thinking.

Another activity that Milan suggests using dice is that of building simple buildings using the dice as bricks. To do this you need a number of "congruent" dice - did you know that the spots on dice are not always put on in the same way? Well, your set of six dice need to be the same. Build a dice tower and put it in a "corner" so that you can only see the top of the top die and two sides on each dice. Start off using just two dice and work out how many spots you can see. What is the highest number? What is the lowest? Can you see why? This activity can be extended to dice rows or more complicated buildings. Are there any patterns being generated in the different cases? Milan found that children were highly motivated to build buildings with a given number of spots on the sides and that they could suggest and look for buildings with the smallest number of spots on the building surface. Children were able to find the rules that enabled them to determine the number of spots on view in a tower at a glance.

Routes and pathways

Another scenario involves exploring routes and pathways and moving in various ways through grids. To start with the most familiar setting let us consider moving about on a square grid. We developed this idea into an investigation called Watch Your Feet. The patterns that children could make from this scenario could just be recorded as patterns building up a class display of the possible outcomes. The preparation of lots of strips of paths of different widths would help to facilitate this. It would also be possible to categorise the results. Different criteria for the categorisation could be discussed.

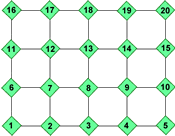Other suggestions include looking at routes through squared grids using colour, say red for right and blue for up, so that different paths can be described by colours simulating the real movement of an object, a person through streets for example. This could be extended to include forward and backward movement and possibly linked with number so that a move to the right horizontally involves adding one and a move vertically upwards involves adding five. This idea was developed into a problem called Routes 1 and 5.

The possibilities are endless but the point, as Milan says, is to develop attractive, simple and understandable tasks that will help to develop the geometric thinking and imagination of young children. As you can see from these examples, the simplest setting can often encourage rich thinking and by offering children geometric contexts as well as numeric ones, we will be offering greater opportunities to engage with mathematics to pupils who have different styles of learning. Non-traditional tasks offer children the chance to explore how to think when they do not know what to do. This quality of thinking seems to me to be far more important than encouraging pupils to engage in the repetition of routine procedures and the proof lies in the children's enthusiasm, motivation and engagement with the task. Try it and see!

REFERENCES

Milan Trch and Eva Zapotilova, (1995), Non-standard Problems: The Means of Development of Thinking and Geometric Imagination in The Lowest School Age. Proceedings of the International Symposium on Elementary Maths Teaching 1995. Charles University, Praha, Czech Republic.

Milan Trch and Eva Zapotilova, (1997), Non-Traditional Mathematical Tasks as a Means of Developing Mathematical Thinking of Younger Children and Problems with their Evaluation. Proceedings of the International Symposium on Elementary Maths Teaching 1997 . Charles University, Praha, Czech Republic.

This article appeared in Primary Mathematics, a journal published by the Mathematics Association , in Summer 2002.