Skip over navigation
You have ten identical open-topped boxes with 10 visually identical coins in each.
In nine of the boxes each of the 10 coins has a mass of 10g.
In one box the 10 coins have masses of only 9g each.
How can you find which box is the odd one out?
Money Measure
Age 7 to 11
Challenge Level 
Money Measure
You have ten identical open-topped boxes with 10 visually identical coins in each.
In nine of the boxes each of the 10 coins has a mass of 10g.
In one box the 10 coins have masses of only 9g each.
How can you find which box is the odd one out?
You have a normal mass measurer with a single pan and a scale. With just one weighing you can identify the box with the lighter coins.
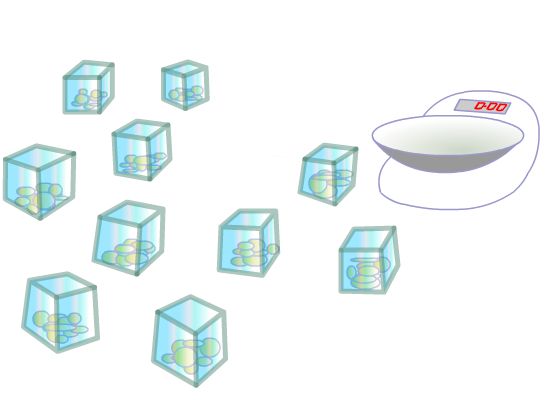
What will you weigh?
Why do this problem?
This problem involves thinking 'out of the box'. The pupils need to work out a way of making one weighing of all the boxes that will give them information about all the different boxes at once.
Possible approach
Key questions
Possible extension
Possible support
You may also like
What's My Weight?
There are four equal weights on one side of the scale and an apple on the other side. What can you say that is true about the apple and the weights from the picture?
Pies
Grandma found her pie balanced on the scale with two weights and a quarter of a pie. So how heavy was each pie?
Oranges and Lemons
On the table there is a pile of oranges and lemons that weighs exactly one kilogram. Using the information, can you work out how many lemons there are?