Skip over navigation
Imagine a (2x2x2) cube made from 8 smaller red cubes. Each small cube has 6 faces, making a total of 6 x 8 = 48 small faces.
On each side of the large cube you can see faces of 4 of the smaller cubes. By turning the large cube around you can see 24 small faces all together.
You dip the cube into a pot of yellow paint and wait for it to dry. Now you separate all the smaller cubes and you can see that 24 of the 48 small faces are yellow and 24 are still red.
This suggests that you can rearrange the cubes so that only red faces are on the outside and yellow on the inside. Then, by dipping the cube into a pot of green paint it seems reasonable to assume you will end up with 8 small cubes whose 48 faces are now all painted yellow or green (24 of each), none that are still red and none that have been painted twice. Is this true?
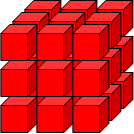
How about a 3 x 3 cube? This will have 27 smaller cubes, making a total of 162 faces, 6 x 9 = 54 being visible at any one time. This suggests you might need three pots of paint to colour all the faces of the smaller cubes without repetition and without having any red faces left.
Is this possible and how would you rearrange the cubes each time? Describe the system you are using.
How about a 4 x 4 x 4 cube and an n x n x n cube?
N.B. This problem is a 3D version of "On the Edge " which can be found on the site.
Inside Out
Age 14 to 16
Challenge Level 
Imagine a (2x2x2) cube made from 8 smaller red cubes. Each small cube has 6 faces, making a total of 6 x 8 = 48 small faces.
On each side of the large cube you can see faces of 4 of the smaller cubes. By turning the large cube around you can see 24 small faces all together.
You dip the cube into a pot of yellow paint and wait for it to dry. Now you separate all the smaller cubes and you can see that 24 of the 48 small faces are yellow and 24 are still red.
This suggests that you can rearrange the cubes so that only red faces are on the outside and yellow on the inside. Then, by dipping the cube into a pot of green paint it seems reasonable to assume you will end up with 8 small cubes whose 48 faces are now all painted yellow or green (24 of each), none that are still red and none that have been painted twice. Is this true?
How about a 3 x 3 cube? This will have 27 smaller cubes, making a total of 162 faces, 6 x 9 = 54 being visible at any one time. This suggests you might need three pots of paint to colour all the faces of the smaller cubes without repetition and without having any red faces left.
Is this possible and how would you rearrange the cubes each time? Describe the system you are using.
How about a 4 x 4 x 4 cube and an n x n x n cube?
N.B. This problem is a 3D version of "On the Edge " which can be found on the site.
You may also like
Just Rolling Round
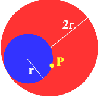
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Coke Machine
The coke machine in college takes 50 pence pieces. It also takes a certain foreign coin of traditional design...
Just Opposite
A and C are the opposite vertices of a square ABCD, and have coordinates (a,b) and (c,d), respectively. What are the coordinates of the vertices B and D? What is the area of the square?