Skip over navigation
Answer: 20%
Using inverse operations
100% + 25% = 1 + $\frac14$ = $\frac54$
speed $\times$ time = distance
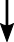$\times \frac54$ 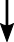$\times$ ? 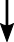$\times$ 1 because distance does not change
(new speed) $\times$ (new time) = distance
$\frac 54 \times$ ? = 1, so ? = $\frac45$ = 80%
80% of original time is a 20% reduction
Using a speed-time graph
The area on a speed-time graph represents distance.
Yellow rectangle - before 1 year training
Green rectangle - after 1 year training
The rectangles have the same area since the distance is still the same
Vertical scale factor $\times$ 125% = 1.25
So horizontal scale factor is the inverse
$\div$ 1.25 = $\div \frac54$ = $\times \frac45$ = $\times$ 80%
80% of original time is a 20% reduction
Using algebra
Before: speed $v$ time $\dfrac{26}{v}$
After: speed $\frac54V$ time $\dfrac{26}{\frac54v}$
$=\dfrac{4\times26}{5v}$
$=\dfrac45\times\dfrac{26}v$
80% of original time is a 20% reduction
Marathon Mission
Age 14 to 16
ShortChallenge Level 
Answer: 20%
Using inverse operations
100% + 25% = 1 + $\frac14$ = $\frac54$
speed $\times$ time = distance
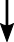$\times \frac54$ $\times$ ? $\times$ 1 because distance does not change(new speed) $\times$ (new time) = distance
$\frac 54 \times$ ? = 1, so ? = $\frac45$ = 80%
80% of original time is a 20% reduction
Using a speed-time graph
The area on a speed-time graph represents distance.
Yellow rectangle - before 1 year training
Green rectangle - after 1 year training
The rectangles have the same area since the distance is still the sameVertical scale factor $\times$ 125% = 1.25
So horizontal scale factor is the inverse
$\div$ 1.25 = $\div \frac54$ = $\times \frac45$ = $\times$ 80%
80% of original time is a 20% reduction
Using algebra
Before: speed $v$ time $\dfrac{26}{v}$
After: speed $\frac54V$ time $\dfrac{26}{\frac54v}$
$=\dfrac{4\times26}{5v}$
$=\dfrac45\times\dfrac{26}v$
80% of original time is a 20% reduction
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
