Going Places with Mathematicians

The idea of representing places and spaces is very important in mathematics. It is important to us all if we don't want to keep losing things - especially ourselves as we move from one place to another. Many famous mathematicians have spent time working on problems that involve moving and mapping things. Some of them have come up with ideas that have helped us find our way around the world, others have designed intriguing puzzles based on moving around.

Rene Descartes was one of those people. Descartes was a French mathematician, philosopher, and anatomist who lived from 1596 to 1650. He contributed to many modern ideas, mainly those associated with science and the scientific method. He developed a design for an improved telescope and mapped the pathway of nerves from the eye to the optical centre in the brain and traced the path of pain receptors from limbs to the brain.

One of the things that Rene Descartes is most famous for is The Cartesian Coordinate System that is named after him. It is interesting how Descartes came to develop Cartesian coordinates. He was lying on his bed watching a fly!

Slowly, it came to him that he would be able to accurately describe the fly's position at any time by just three numbers. He had to use three numbers because the room was three-dimensional. The three numbers would describe the fly's position in relation to where it was to the floor and two adjacent walls. Today this is known as the x,y,z coordinate system. Most modern cities are laid out in Cartesian fashion, tell a stranger to go three blocks down the Main Street and then turn right on Jackson Avenue and go along 10 blocks and you are actually using Cartesian coordinates. If you have been lost in an old town, or even in new developments, you will understand how useful The Cartesian Coordinate System is. The system is used by the military and rescue services as well as air traffic controllers and map makers to accurately describe where to find people and places.

As a mathematician Descartes was credited with developing the system that still serves as the foundation for graphing some 350 years after his death.

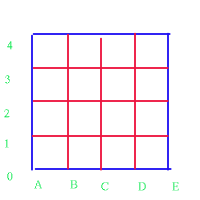
If you ever play `battleships' then you are using cartesian coordinates. To set up the grid people often use a system of letters and numbers. This way you can describe a particular point on the grid. For instance X here is at (C,2). To make sure people communicate information in the same way, we have a system for giving the location of a point. We give the horizonal information first followed by the vertical. You will find a grid like this as the board in the Criss Cross Quiz game .

This is also the same system used for constructing graphs. Rene Descartes' coordinates are the foundation for graphing. Most graphs use a grid with only numbers to show positions. In the lower left corner is a point called the origin, this is the beginning of the graph and it is at the point located at (0,0). The bottom line of the graph and the line at the left hand side of the graph are known as the x and y axes (plural of axis). The x axis runs horizontally, the y axis vertically, and locations within the graph are described using (x,y) pairs. It's easy to remember the order that you name the points because x comes before y in the alaphabet. Other graphs show specific information along the x and y axes depending on what the graph is trying to convey.

More than 350 years after his death, Rene Descartes' system of describing the position or location of things is still very important in many different ways.

Another mathematician who was interested in problems concerning motion and maps was Leonard Euler who lived in the 1700's in Switerland and then later in Russia. He is remembered today for his work in a new branch of mathematics called topology.

Topologists are mathematicians who study problems and puzzles about geometrical structures. Topology sometimes gets called 'rubber sheet geometry' - because topologists study the properties of shapes that stay the same when the shapes are stretched or squashed.

They don't ask questions such as, How big is it? They are much more interested in answering unusual questions like; Are there any holes in it? Are all the parts connected together? Can the whole thing be separated into smaller parts? One example of what topologists might be interested in is a network - like a network of train lines that cross each other and have certain points where the lines come together and then separate. If you made a plan of a rail network on a rubber sheet and stretched it or squashed it up, while the map might look funny, it does not change the plan of the network.

So, if topologists were using the map of the London Underground network they wouldn't be investigating how far it is from Kings Cross to Paddington, or even the direction you are travelling in. They would probably be looking to see if the underground lines connect up and how many different ways you can travel to the same station without passing through the same place twice.

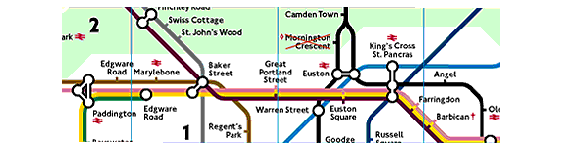
Euler worked on and created problems about networks. He designed a very famous problem based on a town, a river and a network of bridges. You can read about it here .