All Is Number

During the school year you are often asked, in different areas of the curriculum, to research the life of and write a report about somebody who has greatly influenced life and learning . You may be asked to describe the work of a famous mathematician and how that influences what you learn in mathematics today. You might be required in social studies to choose a person who has had a huge impact on many cultures and many people throughout time. It could be that for a science project you investigate the life of a scientist, such as an astronomer, who made important discoveries about what we know today about our earth or other planets. Or perhaps the music teacher will set you an assignment to discover a character who made a musical breakthrough. For any one of these assignments you could select the same person to study, Pythagoras .

Usually, when we hear the name Pythagoras, or more formally Pythagoras of Samos, we think of right-angled triangles or the hypotenuse and maybe squares and things! But there was a lot more to Pythagoras than his famous theorem.
 

He was well known in his day, enough that statues of him were sculptured and drawings and paintings made. If you look for information about him at a maths history site, like the wonderfully informative one produced by St Andrew's University , you will discover that after Nash, Einstein and Newton, Pythagoras' is the most requested biography of a mathematician. He lived from about 580 BC to about 500 BC in Greece, we can't be sure exactly, but it was a long time ago and we are as fascinated by him today as people in his time were.


 

Little is known of Pythagoras' childhood. The only description of how he looked that is probably true is the description of a noticeable birthmark on his thigh! Information differs, some sources say that he had two brothers, although others state it was three. What they agree on is that he was well educated; he was a fine musician, he played the lyre and used music to help people who were ill; he learned poetry and was able to recite famous and popular Greek writers like Homer. While he was a young student, three teachers who were philosophers greatly influenced Pythagoras.

When he was between 18 and 20 years old, Pythagoras left Greece and went to a town called Miletus, which is in the country we now call Turkey, and visited an old man named Thales.

Thales made a big impression on him and advised Pythagoras to travel to Egypt. While he was there he visited many temples and took part in discussions with the priests and learned from some of Thales' pupils about geometry and cosmology. Because of the people he met and the experiences he had, Pythagoras became a philosopher like his teachers, but went on to make important discoveries in mathematics, astronomy, and the theory of music.

In 525 BC, after a battle between the king of Persia and the Egyptians,

Pythagoras was taken prisoner and taken to Babylon where he continued his quest for learning new things. He was instructed in the sacred rites of the Babylonians and learnt about their mystical worship of the gods. He perfected his skills in music and arithmetic as well as the other mathematical sciences taught by the Babylonians.


 

Although he was a very important figure in the development of mathematical ideas, we don't know much about Pythagoras' actual mathematical achievements. Unlike many other Greek mathematicians, none of his writings exist to provide evidence about his interests. Fortunately, many other people wrote about him and his work and from them we know that Pythagoras was really into numbers in a big way! In fact, he thought numbers had personalities - he regarded each one as either masculine or feminine, perfect or incomplete, beautiful or ugly. This number interest probably came about after his capture by the Babylonians.

Pythagoras was the first to distinguish between odd and even numbers and he came up with the idea of prime numbers and showed how they were different from what we call composite numbers. But ten was the very best number of all: it was the sum of the first four integers one, two, three, and four [1 + 2 + 3 + 4 = 10]. If each of these were represented by a dot notation in a series, one above the other, they formed a perfect triangle. We can add perfect, abundant and deficient as well as triangular numbers to Pythagoras' amazing numbers list.

He worked also on the ratio between numbers and then went on todiscoversome numbers that didn't have ratios, these he called irrational numbers. Of course, we can't forget that he proved a Babylonian idea that was already a thousand years old, that parts of triangles are related in size. This has come to be known as Pythagoras' Theorem .
 

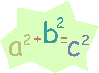
The theorem proves that when the two shorter sides of a right triangle are squared and then added together, the answer is the same as the square of the longest side - or the hypotenuse. Try it and see if you agree!

There are only five regular solid shapes , and it is thought that Pythagoras knew how to construct the first three but unlikely that he was able to construct the other two. If you are not sure what 'regular solid' means you can easily find out . It seems strange today, but being able to construct three solids was quite an achievement in Pythagoras' day and people even wrote about it! For instructions how to construct all five visit a 'net' site .

What clearly made Pythagoras such a great thinker was the fact that he was a great observer. Pythagoras observed that when a string is vibrating, the longer or shorter the string is makes a difference in the pitch of the note. Take a string and twang it. ,try with a string that is just half the length of the first. A string exactly half its length will produce the same note, only one octave higher. If you try with a string twice the length of the original string, the note produced will be one octave lower. Strings whose lengths form ratios equal to, or are in proportion to, whole numbers produce harmonious sounds. This idea led to the development of such things as the thread-board on a guitar.

Pythagoras made remarkable contributions to the mathematical theory of music. I wonder how many guitar players know that mathematics is behind their music!

As an astronomer , Pythagoras was convinced that the Earth was a sphere but thought that it was at the centre of the Universe. Once he was certain that the Earth was a sphere, he was able to deduce that the sun and all the other planets were also spherical and that they moved around each other in circles.
 

Pythagoras obviously had a lot of knowledge to share. He didn't keep it to himself but started a school and a society for other men interested in the same things as he was. The school was called the 'semicircle'. I wonder what shape their seating arrangement was! Pythagoras' followers called themselves the Pythagoreans. Pythagoreans had beliefs and discoveries of their own and, today, we can't tell the difference between their work and Pythagoras'. What the Pythagoreans all had in common is the thought that everything in the cosmos is about numbers.

If you were a Pythagorean, you had to be prepared to follow strict rules. An interesting thing about the school was that you were automatically a Pythagorean too. That meant if you were a student you'd have to obey all the men's rules also.

Have you noticed the word 'men' is used. One rule was, no females allowed! Another rule was silence. This meant that you could not share any of your ideas with others outside the group and that you could only listen to your fellow Pythagoreans. Because they said nothing about what they studied, it was seen as a secret society and people were quite suspicious and afraid of them. Another rule was no eating meat. His followers also believed in reincarnation. Many of these rules and beliefs came from customs Pythagoras had come across in Egypt: for example, the secrets kept by the Egyptian priests, the fact they never ate beans and their refusal to wear any clothes made from animal skins.

Of course, Pythagoras will continue to be remembered mostly for his famous geometry theorem. But we should also remember that his belief that everything can be understood through and explained by mathematics was extremely important to the development of science and mathematics throughout the ages. He influenced the world by his simple expression

All is number ...