Skip over navigation
Trevor from Riccarton High School and Louise from Bourne Grammar School made excellent attempts at solving this puzzle. They both devised good methods for representing the new arrangement of the cards after each turn.
Shaun from Nottingham High School went a step further and realised that it was not necessary to number the cards just indicate whether a given position could or could not hold the chosen card.
Here's how he did that :
The cards are laid out in three columns, five rows.
An O denotes a card the person could have possibly chosen, and X one we are certain they have not.
Here's the first arrangement :

Once the person tells us which column the card is in the first time, this column is put in the middle, so no matter what column the card is in, the cards are laid out like so:
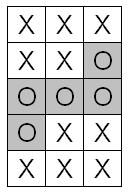
The next time the cards are laid out there are three possibilities. Possibility 1 is that the card is in the left column, possibility 2 that the card is in the centre column, and possibility 3 is that the card is in the right hand column.
When the correct column is put in the centre again, the cards will be laid out in one of the following ways:
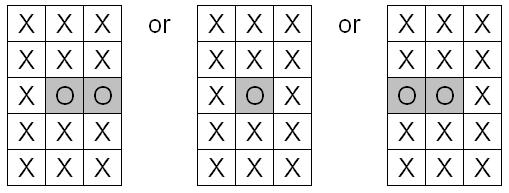
Notice that whatever column the correct card is in, it is always in the third row down. When this correct column is now put in between the two other columns, the correct card becomes the eighth in the pack. This is how the trick works.
Shaun then went on to consider the problem more generally :
For just 3 cards : The column only has to be given once, and the correct card can be found, since there is only one card in each column.
For 6 cards : the correct card can be worked out on the second dealing of the cards. The first deal will put it either on the top row of the right hand column, or the bottom row of the left hand column. When the correct column is then given by the person, the card will be known. However, it will not be possible, like in the 15 card version, to say that it is the nth card in the pack, since it resides on either of the two rows, and will be either the third or fourth. Further repetitions of rearranging the cards do nothing; the correct card stays in the same position.
For 9 cards the trick works exactly as with 15 cards, except only two rearrangements, instead of three, are needed. This is because, after the first rearrangement, the three possible correct cards are all put on the same (middle) row, and so after the person has given the column of their card a second time, it will be put into the middle of the pack, and be the (n + 1)/2 th card.
For 12 cards the case is very similar to that for 6 cards, except one more rearrangement is needed. The correct card will become stuck in one of two possible positions, either left hand column, third row, or right hand column, second row, allowing it to be discovered.
For 21 cards, intuition suggested to me that the number of cards required must be an odd number multiplied by an odd number. Quite amazingly, the trick still works, in the same amount of moves.
For 27 cards I attempted drawing diagrams like the ones above. It still worked.
Then, for 33, the same trick was attempted. It now requires more than three rearrangements to work, and so we can say the highest number of cards the exact trick works for is 27.
This can be explained by looking at the position of possible correct cards after the second rearrangement. In order for the trick to be completed in three rearrangements, the number of rows the possible cards take up can be no more than three. This is because when the correct column is chosen next time, and the now possible correct cards sent into the middle of the pack, they will take up more than one row, and so two or more possibly correct cards will occupy the same column, and it will not be possible to know for certain what the correct card is from the person's next column declaration.
Also, the number of rows the possibly correct cards take up after the first rearrangement must be an odd number, and have equal numbers of rows which contain only cards which cannot possibly be the correct card in them both above and below them, hence why the trick does not work for numbers of cards made up of an even times and odd number. This is because the number of possibly correct cards will be a third of the total cards. Because they are in the middle of the pack, they will take up the middle row, and then work their way outwards to those immediately above and below it. However, as I said and explained above, they cannot extend to more than three rows high in order to complete the trick in three rearrangements.
Well done Shaun


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Spot the Card
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
Trevor from Riccarton High School and Louise from Bourne Grammar School made excellent attempts at solving this puzzle. They both devised good methods for representing the new arrangement of the cards after each turn.
Shaun from Nottingham High School went a step further and realised that it was not necessary to number the cards just indicate whether a given position could or could not hold the chosen card.
Here's how he did that :
The cards are laid out in three columns, five rows.
An O denotes a card the person could have possibly chosen, and X one we are certain they have not.
Here's the first arrangement :
Once the person tells us which column the card is in the first time, this column is put in the middle, so no matter what column the card is in, the cards are laid out like so:
The next time the cards are laid out there are three possibilities. Possibility 1 is that the card is in the left column, possibility 2 that the card is in the centre column, and possibility 3 is that the card is in the right hand column.
When the correct column is put in the centre again, the cards will be laid out in one of the following ways:
Notice that whatever column the correct card is in, it is always in the third row down. When this correct column is now put in between the two other columns, the correct card becomes the eighth in the pack. This is how the trick works.
Shaun then went on to consider the problem more generally :
For just 3 cards : The column only has to be given once, and the correct card can be found, since there is only one card in each column.
For 6 cards : the correct card can be worked out on the second dealing of the cards. The first deal will put it either on the top row of the right hand column, or the bottom row of the left hand column. When the correct column is then given by the person, the card will be known. However, it will not be possible, like in the 15 card version, to say that it is the nth card in the pack, since it resides on either of the two rows, and will be either the third or fourth. Further repetitions of rearranging the cards do nothing; the correct card stays in the same position.
For 9 cards the trick works exactly as with 15 cards, except only two rearrangements, instead of three, are needed. This is because, after the first rearrangement, the three possible correct cards are all put on the same (middle) row, and so after the person has given the column of their card a second time, it will be put into the middle of the pack, and be the (n + 1)/2 th card.
For 12 cards the case is very similar to that for 6 cards, except one more rearrangement is needed. The correct card will become stuck in one of two possible positions, either left hand column, third row, or right hand column, second row, allowing it to be discovered.
For 21 cards, intuition suggested to me that the number of cards required must be an odd number multiplied by an odd number. Quite amazingly, the trick still works, in the same amount of moves.
For 27 cards I attempted drawing diagrams like the ones above. It still worked.
Then, for 33, the same trick was attempted. It now requires more than three rearrangements to work, and so we can say the highest number of cards the exact trick works for is 27.
This can be explained by looking at the position of possible correct cards after the second rearrangement. In order for the trick to be completed in three rearrangements, the number of rows the possible cards take up can be no more than three. This is because when the correct column is chosen next time, and the now possible correct cards sent into the middle of the pack, they will take up more than one row, and so two or more possibly correct cards will occupy the same column, and it will not be possible to know for certain what the correct card is from the person's next column declaration.
Also, the number of rows the possibly correct cards take up after the first rearrangement must be an odd number, and have equal numbers of rows which contain only cards which cannot possibly be the correct card in them both above and below them, hence why the trick does not work for numbers of cards made up of an even times and odd number. This is because the number of possibly correct cards will be a third of the total cards. Because they are in the middle of the pack, they will take up the middle row, and then work their way outwards to those immediately above and below it. However, as I said and explained above, they cannot extend to more than three rows high in order to complete the trick in three rearrangements.
Well done Shaun
You may also like
Fixing the Odds
You have two bags, four red balls and four white balls. You must put all the balls in the bags although you are allowed to have one bag empty. How should you distribute the balls between the two bags so as to make the probability of choosing a red ball as small as possible and what will the probability be in that case?
Scratch Cards
To win on a scratch card you have to uncover three numbers that add up to more than fifteen. What is the probability of winning a prize?
Escalator
At Holborn underground station there is a very long escalator. Two people are in a hurry and so climb the escalator as it is moving upwards, thus adding their speed to that of the moving steps. ... How many steps are there on the escalator?

