Skip over navigation

The Thousands Game

Age 7 to 11

Challenge Level Yellow star

Primary curriculum

The Thousands Game

The Thousands Game printable sheet

Class 3 were playing a game. There were ten cards with the digits $0$ to $9$ on them.

These cards were put into a bag and players took out four cards and made a number out of them. At first they made the highest number they could. Sinita took out

and made

Then they made the lowest number they could. Jamie took out

and made

"You can't put zero at the beginning of a number," objected Paul. The class discussed this and decided that Jamie had made four hundred and fifty-seven.

Next they played to make the highest even number. Jill took out

and Vincent took out

Who won? Why?

Then they played to make the highest odd number. Belinda took out

and Ali took out

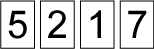
Who won? Why?

Next they played to make the lowest even number. Rohan took out

and Ben took out

Who won? Why?

The last game they played was to make the closest number to $5000$. Alice took out

and Chloe took out

Who won? Why?

Play some of the different versions of this game with a friend. Which digits are the most helpful? Why?

Once you've played this game a few times, have a go at playing Nice or Nasty. This game is very similar except you draw and place the digits one at a time, so you'll need to think carefully about where to put each one!

Why do this problem?

This problem can be used when introducing or revising numbers in the thousands. Children's understanding of place value will be reinforced and discussion will give plenty of opportunities to emphasise appropriate vocabulary not only on place value but also on odd and even numbers. The game described can transform what could be a tedious task into an engaging activity.

Possible approach

You could start by playing the game described in the problem with the whole group. You will need a set of digit cards. This sheet of digit cards can be printed out, preferably onto card. A bag is not necessary, but does add a little drama into the activity! The important thing is that the cards should be picked unseen. This simple interactivity can be used for displaying the digit cards when they have been chosen. It should be noted that the cards (and bag) will still be required.

After this learners could work in pairs on the game. This sheet provides two "boards" for playing the game with the digit cards provided. Then they could go on to the actual problem from this sheet which gives the questions asked (but without the introduction).

At the end of the lesson the group can gather together to discuss, not only place value and comparing and ordering numbers, but also odd and even numbers. There should be plenty of opportunities to emphasise the appropriate vocabulary for the work they have been doing.

Key questions

Which digit is most important if you are making the largest/smallest number possible?

To make the highest possible number, where would it be best to put the highest/lowest digit card?

If you want to make the lowest number, where would it be best to put the lowest/highest digit card?

What makes a number odd/even?

What kind of number will the units digit need to be to make an even number? What about an odd number?

Possible extension

Learners could play an alternative version of the game in which two players take turns in taking a digit card (unseen) and placing it on their board before taking the next card. This requires considerable thought and understanding. Children will enjoy playing Nice and Nasty after having a go at this activity.

Possible support

Some children find place value difficult and even alarming. They could start with a similar activity using only three-digit numbers or even just two. Reading the numbers out loud may help turn what seems to them just a jumble of digits into something meaningful.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

The Thousands Game

The Thousands Game

Why do this problem?

Possible approach

Key questions

Possible extension

Possible support

You may also like

Number Detective

Six Is the Sum

ABC