Skip over navigation
A 50 pence piece is a 7 sided
polygon ABCDEFG with rounded edges, obtained by replacing the
straight line DE with an arc centred at A and radius AE; replacing
the straight line EF with an arc centred at B radius BF
...etc..
The 50p piece can roll in the same chute as a disc of radius $r$. Suppose the seven arcs forming the edge of the 50p piece (the arcs AB, BC etc. ) all have radius $R$ (where $R$=AD=AE=BE=BF...) then you need to find $R$ in terms of $r$. These seven arcs subtend angles of $2\pi /7$ at the centre of the disc and $2\pi /14$ at the opposite edge.
Coke Machine
Age 14 to 16
Challenge Level 
This is another tough nut and perhaps the diagram of the 50p piece will help.
The 50p piece can roll in the same chute as a disc of radius $r$. Suppose the seven arcs forming the edge of the 50p piece (the arcs AB, BC etc. ) all have radius $R$ (where $R$=AD=AE=BE=BF...) then you need to find $R$ in terms of $r$. These seven arcs subtend angles of $2\pi /7$ at the centre of the disc and $2\pi /14$ at the opposite edge.
You may also like
Just Rolling Round
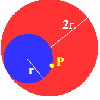
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Just Opposite
A and C are the opposite vertices of a square ABCD, and have coordinates (a,b) and (c,d), respectively. What are the coordinates of the vertices B and D? What is the area of the square?
