Skip over navigation
Billy's school has a paved area at the front:
Billy's class had a robot called Fred who could draw with chalk held underneath him.
Billy's teacher drew lines and numbers on the paved area in front of the school so that they could tell Fred where to go.
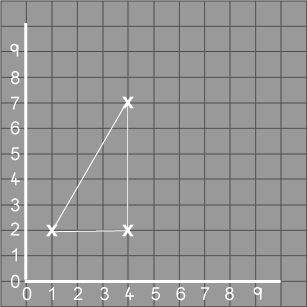
Billy's teacher put a little cross on the point $(1, 2)$ and the children put Fred on the cross. Fred moved to $(4, 7)$, then to $(4, 2)$ and then back to $(1, 2 )$. Fred's chalk drew a line to show where he had been.
Fred the Class Robot
Age 7 to 11
Challenge Level 
Fred the Class Robot
Billy's school has a paved area at the front:
Billy's class had a robot called Fred who could draw with chalk held underneath him.
Billy's teacher drew lines and numbers on the paved area in front of the school so that they could tell Fred where to go.
Billy's teacher put a little cross on the point $(1, 2)$ and the children put Fred on the cross. Fred moved to $(4, 7)$, then to $(4, 2)$ and then back to $(1, 2 )$. Fred's chalk drew a line to show where he had been.
"What shape has Fred drawn?" asked Billy's teacher.
"A triangle!" shouted all the class.
All the children wanted to make Fred draw shapes.
Tom had the first turn. He got Fred to go from $(6, 1)$ to $(6, 6)$, and then to $(1, 6)$ and $(1, 1)$ and back to $(6, 1)$.
What shape had Fred drawn?
Vicky made Fred go from $(2, 1)$ to $(7, 2)$, and then to $(9, 4)$ and $(4, 6)$ and then $(1, 5)$ and back to $(2, 1)$.
What shape had Vicky made Fred draw?
Billy thought very hard when it was his turn. He made Fred go from $(7, 4)$ to $(4, 7)$, and then to $(1, 4)$ and $(4, 1)$ and back to $(7, 4)$.
What shape had Billy made Fred draw?
If Billy had made Fred start at the same place, $(7, 4)$, how else could a shape like this be drawn on the $9$ by $9$ axes? (It doesn't have to be the same size as Billy's first shape.)
Why do this problem?
This problem is one in which learners will be practising the use of coordinates and in addition will be developing their understanding of properties of shapes. The problem may challenge their preconceptions of how a shape "should be" oriented!
A similar activity could be set up practically in the classroom or outside using a floor turtle. In any case squared paper should be provided.
Key questions
Would it help to draw out what Fred is doing on squared paper?
Have you counted the number of sides of each shape and looked at the angles?
What makes the shape a square and not another four-sided shape?
Possible extension
Learners could make their own shapes on squared paper and write down the coordinates.Possible support
Suggest drawing the shapes on squared paper. Moving the paper around might help in seeing what each shape is.You may also like
The Lily Pond
Freddie Frog visits as many of the leaves as he can on the way to see Sammy Snail but only visits each lily leaf once. Which is the best way for him to go?
A Cartesian Puzzle
Find the missing coordinates which will form these eight quadrilaterals. These coordinates themselves will then form a shape with rotational and line symmetry.
Transformation Tease
What are the coordinates of this shape after it has been transformed in the ways described? Compare these with the original coordinates. What do you notice about the numbers?