Skip over navigation
On the graph below there are $34$ marked points.
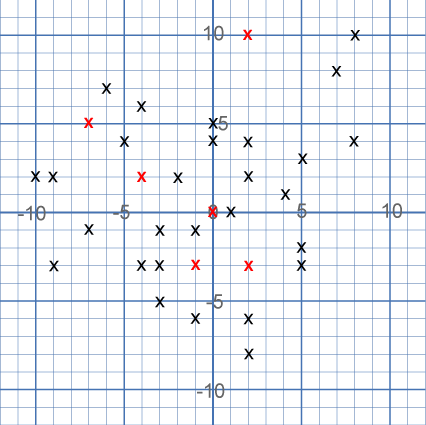
These points all mark the vertices (corners) of ten hidden squares. Each of the $6$ red points is a vertex shared by two squares. The other $28$ points are each a vertex of just one square. All of the squares share at least one vertex with another square.
All the squares are different sizes.
There are no marked points on the sides of any square, only at the vertices. (There are two near misses!)
Can you find the ten hidden squares?
You might like to play the game Seeing Squares which uses some similar ideas.
Ten Hidden Squares
Age 7 to 14
Challenge Level 
On the graph below there are $34$ marked points.
These points all mark the vertices (corners) of ten hidden squares. Each of the $6$ red points is a vertex shared by two squares. The other $28$ points are each a vertex of just one square. All of the squares share at least one vertex with another square.
All the squares are different sizes.
There are no marked points on the sides of any square, only at the vertices. (There are two near misses!)
Can you find the ten hidden squares?
You might like to play the game Seeing Squares which uses some similar ideas.
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.
