Skip over navigation
Kim: $2, 8, 14, 20, 4, 10, 16, 22, 6, 12, 18, 24.$
Butterfly Cards
Age 7 to 11
Challenge Level 
Three groups of children put a lot of thought into this problem. They were: Ella, Luke, Richard and Sebastian from St Nicolas CE Junior School; Jessica and Emily from Aldermaston CE Primary and Burcu from FMV Ozel Erenkoy Isik Ilkogretim Okulu in Turkey.
The pupils from St Nicolas and Burcu started in the same way by numbering the cards as the hint suggests:
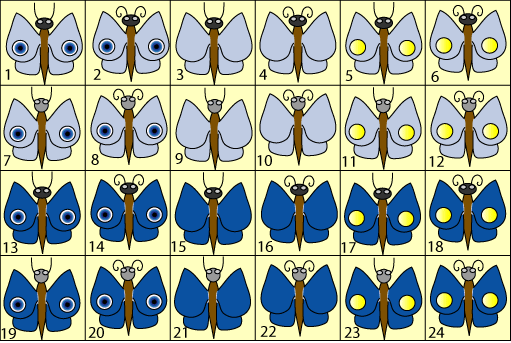
Burcu said:
According to the wishes of Kim, Wim, Jim and Tim they can have the following cards:Kim: $2, 8, 14, 20, 4, 10, 16, 22, 6, 12, 18, 24.$
Wim: $7, 8, 9, 10, 11, 12, 19, 20, 21,
22, 23, 24.$
Jim: $5, 11, 17, 23, 6, 12, 18,
24.$
Tim: $13, 14, 19, 20.$
Jim's complaint is not right, because Jim
wants to have two properties, it does not mean that, he'll get more
cards.
Nobody wants the cards numbered as $1,
3$, and $15$.
There is no card that all the children
want.
Kim wants just the cards $16, 2,
4$.
Jim wants just the cards $5, 17$.
Wim wants just the cards $7, 9,
21$.
Tim wants just the card $13$.
All children can not have the cards they
want.
Pupils from St Nicolas School wrote:
We found it easier to cut out the cards to find out how to share them out fairly. We had two ways which we thought were fair.1) Everyone gets four cards they want and two cards they don't
want e.g.
Kim - $2, 6, 8, 10$ she wants and $9$ and
$15$ she doesn't want.
Wim - $7, 12, 21, 22$ she wants and $5$
and $16$ she doesn't want.
Tim - $13, 14, 19, 20$ he wants and $4$ and $23$ he doesn't want.
Tim - $13, 14, 19, 20$ he wants and $4$ and $23$ he doesn't want.
Jim - $11, 17, 18, 24$ he wants and $1$
and $3$ he doesn't want.
2) Kim, Wim and Jim get five cards they
like and Tim has four cards he likes and two cards he half likes
which would make one he likes and one he doesn't. e.g.
Kim - $2, 4, 6, 16, 18$ and $3$ she
doesn't like.
Wim - $7, 9, 10, 21, 22$ and $5$ she
doesn't like.
Tim - $13, 14, 19, 20$ and $1$ and $15$
he half likes.
Jim - $11, 12, 17, 23, 24$ and $2$ he
doesn't like.
Jessica and Emily used a similar method to try to share out the butterflies. They said:
Our final choice was to give them the
closest to what they wanted.
We tried to be systematic and give the
people at least four of what they wanted first, then five then
six.
We did Tim first because there are only
four of his choice anyway.
Next we did Jim, because there are only
eight of his choice and we tried not to choose curly antennae
because Kim wanted those.
Next we did Wim because he didn't want
the ones with oval heads.
Finally, we did Kim and we gave her any
curly antennae we could find.
Another possibility would be to change the features that the children want. Burcu suggested that the butterflies could be shared in the following way:
If someone wants the butterflies which have oval heads and
light blue wings (six butterflies) ($1, 2, 3, 4, 5, 6$)
If someone wants the butterflies which
have not oval heads and light blue wings (six butterflies) ($7, 8,
9, 10, 11, 12$)
If someone wants the butterflies which
have oval heads and dark blue wings (six butterflies) ($13, 14, 15,
16, 17, 18$)
If someone wants the butterflies which
have not oval heads and dark blue wings (six butterflies) ($19, 20,
21, 22, 23, 24$)
Such a sharing can be a fair way, and
everyone can take the butterflies she/he wants.
You may also like
Cereal Packets
How can you put five cereal packets together to make different shapes if you must put them face-to-face?