Skip over navigation
Miss Brown was working with Becky's group on numbers that share a certain property. She wrote twelve numbers on the board.
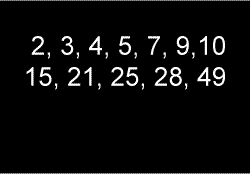
"You can all find a different set of just four numbers that go together," she said, "And they must have a proper mathematical name. They can't be just a set of numbers that you like!"
The children stared at the numbers. Alan put up his hand. "Like odd numbers?" he suggested.
"That's the right idea," said Miss Brown, "but you can't choose just odd numbers because there are more than four of them. You must use all the numbers in my list which fit your set. Anyone else got an idea?"
Becky put her hand up. "Numbers in the $5$ times table? There are four of those."
"That's right. But what would be a good name for them?"
"Multiples of $5$?" suggested Becky.
"Good," said Miss Brown and she wrote on the board:
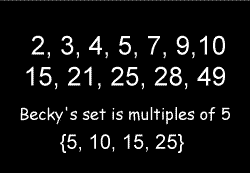



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Sets of Four Numbers
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Sets of Four Numbers
Miss Brown was working with Becky's group on numbers that share a certain property. She wrote twelve numbers on the board.
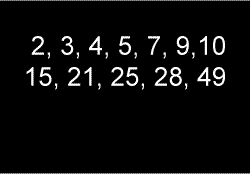
"You can all find a different set of just four numbers that go together," she said, "And they must have a proper mathematical name. They can't be just a set of numbers that you like!"
The children stared at the numbers. Alan put up his hand. "Like odd numbers?" he suggested.
"That's the right idea," said Miss Brown, "but you can't choose just odd numbers because there are more than four of them. You must use all the numbers in my list which fit your set. Anyone else got an idea?"
Becky put her hand up. "Numbers in the $5$ times table? There are four of those."
"That's right. But what would be a good name for them?"
"Multiples of $5$?" suggested Becky.
"Good," said Miss Brown and she wrote on the board:
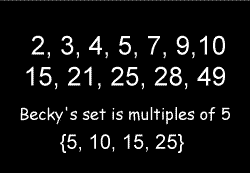
There are ten children in Becky's group.
Can you find a set of numbers for each of them?
Are there any other sets?
Why do this problem?
This problem can be used at any time when learners are looking at varied properties of numbers. There are a large number of possibilities so the problem can be as challenging as you want!Possible approach
Here are two suggestions of ways you could start the lesson.
Firstly, you could begin by writing down some numbers on the board and asking for those with the same properties. These eight numbers, for example, could be used: $5, 9, 12, 16, 20, 24, 30, 35$. Remember that in the problem that there must be four, and only four, numbers in a certain category. In this list there are five even numbers to help in making this point. Alternatively, you could
begin with the problem itself as given.
In both cases it will be necessary to make sure that learners know that there must only be four numbers chosen from the list and that each number can be used in as many sets as they want. They should also find a title for their set such as "multiples/factors of ... " or "single digit numbers".
After the introduction learners could work in pairs on the problem so that they are able to talk through their ideas with a partner.
At the end of the lesson you could write all the different categories that have been found on the board, or on paper on a designated section of the classroom walls. You should have many more than just ten. The advantage of creating a wall display is that it can become interactive, with learners continuing to add to the list over the coming week.
Key questions
Are there just four numbers that share this property in the list, or are there more than four?
Is this number odd or even?
Which multiplication tables will you find this number in?
What properties does this number have? Are there any others like it?
Can you think of a number that has many factors that you could try? Let's see if any of the numbers on our list are factors of that number.
Have you thought of a title for this set?
Possible extension
Learners could be challenged to find two or more criteria for the same set of numbers.
Possible support
You could suggest writing down the numbers and then underlining all the even numbers in, for example, red. Then circling the multiples of three in another colour and so on. This should highlight several sets of four numbers.You may also like
Worms
Place this "worm" on the 100 square and find the total of the four squares it covers. Keeping its head in the same place, what other totals can you make?
Which Scripts?
There are six numbers written in five different scripts. Can you sort out which is which?
Highest and Lowest
Put operations signs between the numbers 3 4 5 6 to make the highest possible number and lowest possible number.

