Efficient Cutting

Ysanne and Joanna from Central Newcastle High School sent us their thoughts:

Roughly half of the paper should be used to make the circles and roughly half to make the rectangle as the height of the cylinder and the area of the circle are equally important in creating the volume.

We decided to use the side of length $29.6$ as the circumference of the cylinder. As this was the circumference of the cylinder, and therefore the circles, we divided $29.6$ by $\pi$ to find the appropriate diameter for the circles. This came to $9.42$, so the remaining paper left for the rectangle meant that the height of the cylinder would be 11.58. To find the volume, we found the area of the circle and multiplied by the height of the cylinder: $\pi \times 4.71^2 \times 11.58 \approx 807.5$ cubic centimetres as our volume.

Lyman from Nanjing International School sent us this different arrangement and another similar arrangement for the circles and rectangles to try to maximise the area - click here to see them.

Aleksei's students at CIS Russia used the original sides of the A4 sheets of paper to be the heights of the cylinders, rather than the circumferences of the circles. They managed to get even larger areas:

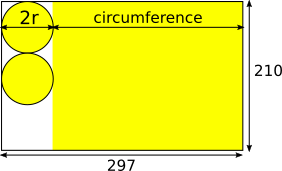
$\begin{align}&C = 2\pi r = 210 - 2r\\ \Rightarrow &2\pi r +2r = 210\\ \Rightarrow & 2(\pi + 1)r = 210 \\ \Rightarrow & r = 210\div((\pi + 1)\times2)\\ \Rightarrow & r =  25.353 \end{align}$

This gives volume:

$V = \pi r^2h = \pi\times25.353^2\times297 = 599722$ cubic millimetres, or $599.7$ cubic centimetres.

Or:

$\begin{align}&C = 2\pi r = 297 - 2r\\ \Rightarrow &2\pi r +2r = 297\\ \Rightarrow & 2(\pi + 1)r = 297 \\ \Rightarrow & r = 297\div((\pi + 1)\times2)\\ \Rightarrow & r =  35.856 \end{align}$

This gives volume:

$V = \pi r^2h = \pi\times35.856^2\times297 = 848178$ cubic millimetres, or $848.2$ cubic centimetres.

Note that taking the longer side of the A4 sheet of paper to be 296mm instead of 297mm gives the volume as 842.4 cubic centimetres.