Skip over navigation
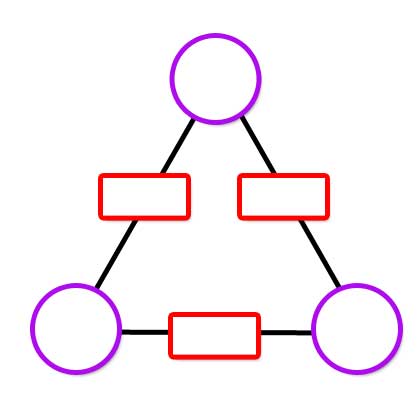
An arithmagon is a polygon with numbers at its vertices which determine the numbers written on its edges.
Check you understand how the values at the vertices determine the values on the edges in the arithmagons generated by the interactivity:
Arithmagons
Age 11 to 16
Challenge Level 
An arithmagon is a polygon with numbers at its vertices which determine the numbers written on its edges.
Check you understand how the values at the vertices determine the values on the edges in the arithmagons generated by the interactivity:
5
1
1
If you are given the values on the edges, can you find a way to work out what values belong at the vertices?
Use the interactivity below to test out your strategies.
There are four different challenge levels to try.
26
9
21
Once you are confident that you can work out the values at the vertices efficiently, here are some questions you might like to consider:
- Can you describe a strategy to work out the values at the vertices irrespective of the values given for the edges?
- By looking at the numbers on the edges, how can you predict whether the numbers at the vertices will all be positive?
- By looking at the numbers on the edges, how can you predict whether the numbers at the vertices will all be whole numbers?
- What happens to the numbers at the vertices if you increase one or more of the numbers on the edges by 1? By 2? ... By n?
- What relationships can you find in square arithmagons? Or pentagonal arithmagons?
A poster of this resource is available here.
You may also like
Rudolff's Problem
A group of 20 people pay a total of £20 to see an exhibition. The admission price is £3 for men, £2 for women and 50p for children. How many men, women and children are there in the group?
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?