Skip over navigation
Well done to Jeremy from the Raffles Institution in Singapore for your well-reasoned solution:
It is only possible when there are 0, 4 or 6 counters.
Recognize that having an odd number of counters would result in a certain number of rows and columns having an odd number of counters. With this in mind, all examples with odd number of counters can be skipped.
When there are 0 counters, there are will be 0 counters on every square. (Remember zero is an even number!)
If only two counters are placed, at least 2 rows/columns would have an odd number of counters as if two counters are placed in the same row, two columns would have an odd number of counters and vice versa.
Example:
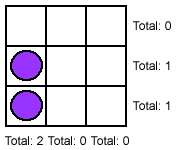
If 4 counters are placed, they can be placed in various positions, as long as there is one empty row and column. If they are placed in 3 rows and columns, there would be certain rows/columns with an odd number of counters.
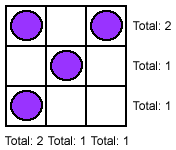
Example, with counters in 3rows and 3 columns:
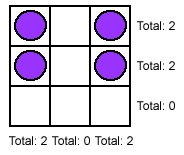
Example, with one row and one column empty:
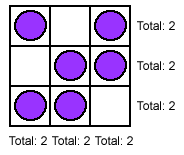
6 is the most number of counters that can be placed as putting any more would result in a line of 3. To do it, fill in all but one square in each row and column.
Example:
Arrangements
Age 7 to 11
Challenge Level 
Well done to Jeremy from the Raffles Institution in Singapore for your well-reasoned solution:
It is only possible when there are 0, 4 or 6 counters.
Recognize that having an odd number of counters would result in a certain number of rows and columns having an odd number of counters. With this in mind, all examples with odd number of counters can be skipped.
When there are 0 counters, there are will be 0 counters on every square. (Remember zero is an even number!)
If only two counters are placed, at least 2 rows/columns would have an odd number of counters as if two counters are placed in the same row, two columns would have an odd number of counters and vice versa.
Example:
If 4 counters are placed, they can be placed in various positions, as long as there is one empty row and column. If they are placed in 3 rows and columns, there would be certain rows/columns with an odd number of counters.
Example, with counters in 3rows and 3 columns:
Example, with one row and one column empty:
6 is the most number of counters that can be placed as putting any more would result in a line of 3. To do it, fill in all but one square in each row and column.
Example:
You may also like
Prime Magic
Place the numbers 1, 2, 3,..., 9 one on each square of a 3 by 3 grid so that all the rows and columns add up to a prime number. How many different solutions can you find?
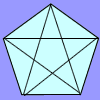
Diagonal Trace
You can trace over all of the diagonals of a pentagon without lifting your pencil and without going over any more than once. Can the same thing be done with a hexagon or with a heptagon?