Skip over navigation
This solution came from Joseph of Colyton Grammar School. Also Yosef who has just graduated from High School and Andrei from Tudor Vianu National College, Bucharest, Romania sent in good solutions.
Supposing that the sequence of continued fractions does tend to a limit $L$ as $n \to \infty$ such that $X_{n+1} = X_n = L$ then, since $$X_{n+1} = {1\over 1+X_n },$$ we can say that: $L=1/(1+L)$ and therefore rearranging gives the quadratic equation $L^2+L-1=0$. Solving this using the quadratic formula gives $$L={-1+ \sqrt5 \over 2}$$ I discarded the negative root because the limit must be positive since we are summing positive fractions.
By taking the positive root of the equation $X^2-X-1=0$ I found the golden ratio $$\phi = {1+ \sqrt 5\over 2}$$ and so $$\phi -1 = {-1+ \sqrt5 \over 2} = L$$ and $${1\over \phi} = {2\over (1+ \sqrt 5)}.$$ By multiplying the numerator and the denominator by $1-\sqrt 5$: $$\eqalign { {1\over \phi} &= {2(1-\sqrt 5)\over(-4)} \cr &= {-1+ \sqrt 5\over 2} = L.}$$ Therefore the limit $L$ of the continued fraction $X_n$ (as $n\to \infty$) is equal to ${1\over \phi}$ where $\phi$ is the golden ratio.
I used induction to prove each continued fraction is equal to the ratio of two Fibonacci numbers, that is to prove the statement $P(n)$ given by $$P(n): X_n = F_n / F_{n+1}$$ where $F_n$ is a Fibonacci number from the sequence defined by the relation $F_{n+2}=F_{n+1}+F_n$ with $F_1=1$ and $F_2=1$.
$X_1 = 1$ and $F_1 /F_2 = 1/1 =1$, therefore $P(1)$ is true.
Assume that $P(k)$ is true, then $X_k = F_k / F_{k+1}$. By the recurrence relation for the continued fractions $X_{k+1} = 1/ (1 + X_k)$. Hence
$$\eqalign{ X_{k+1}&= {1\over 1+X_k} \cr &= {1\over 1+F_k/F_{k+1}} \cr &= {F_{k+1}\over F_{k+1} + F_k}.}$$
But by the recurrence relation for the Fibonacci sequence $F_{k+2} = F_{k+1} + F_k$ which gives $$X_{k+1}= {F_{k+1}\over F_{k+2}}$$ and hence $P(k+1)$ is true.
Therefore if $P(k)$ is true then $P(k+1)$ is true. But $P(1)$ is true and so, by the axiom of mathematical induction, $P(n)$ is true for all positive integers. So we have proved $$X_n = {F_n\over F_{n+1}}.$$ Since we have shown that the limit of $X_n$ (as $n\to \infty$) is $1/\phi$ we have now proved that the limit of $F_n/F_{n+1}= 1/\phi$ (as $n\to \infty$) and so the limit (as $n \to \infty$) of $F_{n+1} / F_n$ is $\phi$, the golden ratio.
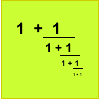
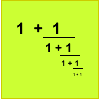
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Golden Fractions
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This solution came from Joseph of Colyton Grammar School. Also Yosef who has just graduated from High School and Andrei from Tudor Vianu National College, Bucharest, Romania sent in good solutions.
Supposing that the sequence of continued fractions does tend to a limit $L$ as $n \to \infty$ such that $X_{n+1} = X_n = L$ then, since $$X_{n+1} = {1\over 1+X_n },$$ we can say that: $L=1/(1+L)$ and therefore rearranging gives the quadratic equation $L^2+L-1=0$. Solving this using the quadratic formula gives $$L={-1+ \sqrt5 \over 2}$$ I discarded the negative root because the limit must be positive since we are summing positive fractions.
By taking the positive root of the equation $X^2-X-1=0$ I found the golden ratio $$\phi = {1+ \sqrt 5\over 2}$$ and so $$\phi -1 = {-1+ \sqrt5 \over 2} = L$$ and $${1\over \phi} = {2\over (1+ \sqrt 5)}.$$ By multiplying the numerator and the denominator by $1-\sqrt 5$: $$\eqalign { {1\over \phi} &= {2(1-\sqrt 5)\over(-4)} \cr &= {-1+ \sqrt 5\over 2} = L.}$$ Therefore the limit $L$ of the continued fraction $X_n$ (as $n\to \infty$) is equal to ${1\over \phi}$ where $\phi$ is the golden ratio.
I used induction to prove each continued fraction is equal to the ratio of two Fibonacci numbers, that is to prove the statement $P(n)$ given by $$P(n): X_n = F_n / F_{n+1}$$ where $F_n$ is a Fibonacci number from the sequence defined by the relation $F_{n+2}=F_{n+1}+F_n$ with $F_1=1$ and $F_2=1$.
$X_1 = 1$ and $F_1 /F_2 = 1/1 =1$, therefore $P(1)$ is true.
Assume that $P(k)$ is true, then $X_k = F_k / F_{k+1}$. By the recurrence relation for the continued fractions $X_{k+1} = 1/ (1 + X_k)$. Hence
$$\eqalign{ X_{k+1}&= {1\over 1+X_k} \cr &= {1\over 1+F_k/F_{k+1}} \cr &= {F_{k+1}\over F_{k+1} + F_k}.}$$
But by the recurrence relation for the Fibonacci sequence $F_{k+2} = F_{k+1} + F_k$ which gives $$X_{k+1}= {F_{k+1}\over F_{k+2}}$$ and hence $P(k+1)$ is true.
Therefore if $P(k)$ is true then $P(k+1)$ is true. But $P(1)$ is true and so, by the axiom of mathematical induction, $P(n)$ is true for all positive integers. So we have proved $$X_n = {F_n\over F_{n+1}}.$$ Since we have shown that the limit of $X_n$ (as $n\to \infty$) is $1/\phi$ we have now proved that the limit of $F_n/F_{n+1}= 1/\phi$ (as $n\to \infty$) and so the limit (as $n \to \infty$) of $F_{n+1} / F_n$ is $\phi$, the golden ratio.
You may also like
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
There's a Limit
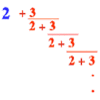
Explore the continued fraction: 2+3/(2+3/(2+3/2+...)) What do you notice when successive terms are taken? What happens to the terms if the fraction goes on indefinitely?
Not Continued Fractions
Which rational numbers cannot be written in the form x + 1/(y + 1/z) where x, y and z are integers?

