Skip over navigation
The solution to this tough nut was submitted by Ray who does not reveal his school.
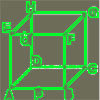
By Pythagoras' Theorem: $$|AB|=\sqrt 3,\ |BC|=\sqrt 2,\ |AC|=\sqrt 5,\ |BD|=\sqrt 5,\ |AD|=\sqrt{10}.$$ As $|AB|^2 + |BC|^2 = |AC|^2$ it follows, by the converse of Pythagoras' Theorem, that $\angle ABC = 90^o$.
Using the cosine rule: $|AD|^2 = |AB|^2 + |BD|^2 - 2|AB||BD|\cos B.$ So $$\cos B= {-1\over \sqrt{15}}$$ and $\angle ABD = 105$ degrees to the nearest degree.
The challenge was to find more than one method so the second method uses geometry and vectors.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cubestick
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
The solution to this tough nut was submitted by Ray who does not reveal his school.
By Pythagoras' Theorem: $$|AB|=\sqrt 3,\ |BC|=\sqrt 2,\ |AC|=\sqrt 5,\ |BD|=\sqrt 5,\ |AD|=\sqrt{10}.$$ As $|AB|^2 + |BC|^2 = |AC|^2$ it follows, by the converse of Pythagoras' Theorem, that $\angle ABC = 90^o$.
Using the cosine rule: $|AD|^2 = |AB|^2 + |BD|^2 - 2|AB||BD|\cos B.$ So $$\cos B= {-1\over \sqrt{15}}$$ and $\angle ABD = 105$ degrees to the nearest degree.
The challenge was to find more than one method so the second method uses geometry and vectors.
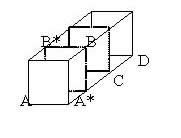 |
Triangle $A^*BC$ is a right angled isosceles triangle and $A^*B$ is perpendicular to $BC$.The line $B^*B$ is perpendicular to the plane $A^*BDC$ so it is perpendicular to $BC$. As the two line $A^*B$ and $B^*B$ are perpendicular to $BC$ the whole plane $AB^*BA^*$ is perpendicular to $BC$. Hence $AB$ is perpendicular to $BC$. |
Using vectors : $$\vec{BA}=(-1,-1,-1),\ \vec{BD} =(2,0,-1).$$ So we find the scalar product: $$ \vec{BA}.\vec{BD} = |BA||BD|\cos B$$ which gives $$ -2+1 = \sqrt 3 \sqrt 5 \cos B.$$ Again: $$\cos B= {-1\over \sqrt{15}}$$ and $\angle ABD = 105$ degrees to the nearest degree.
You may also like
Wrapping Gifts
A box of size a cm by b cm by c cm is to be wrapped with a square piece of wrapping paper. Without cutting the paper what is the smallest square this can be?
Plane to See
P is the midpoint of an edge of a cube and Q divides another edge in the ratio 1 to 4. Find the ratio of the volumes of the two pieces of the cube cut by a plane through PQ and a vertex.
Four Points on a Cube
What is the surface area of the tetrahedron with one vertex at O the vertex of a unit cube and the other vertices at the centres of the faces of the cube not containing O?

