Skip over navigation
This solution was written by Andrei from Tudor Vianu National College, Bucharest, Romania.
I calculate the values of $f(x)= x(x+|x|)$ for $x< 0$ and $x\geq 0$:
$$\eqalign{ f(x) &= x(x-x)=0\ for \ x < 0 \cr &=x(x+x)= 2x^2 \ for \ x\geq 0.}$$
Its graph is represented below: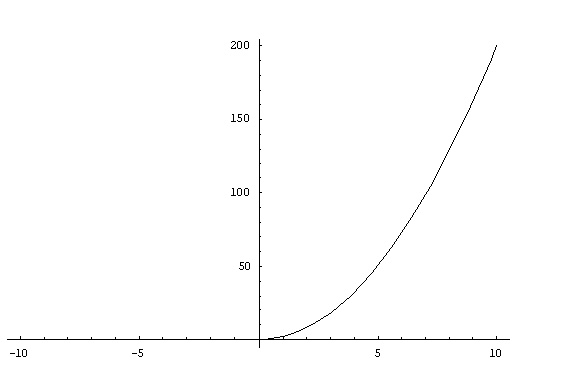

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Slide
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This solution was written by Andrei from Tudor Vianu National College, Bucharest, Romania.
I calculate the values of $f(x)= x(x+|x|)$ for $x< 0$ and $x\geq 0$:
$$\eqalign{ f(x) &= x(x-x)=0\ for \ x < 0 \cr &=x(x+x)= 2x^2 \ for \ x\geq 0.}$$
Its graph is represented below:
Now, I find the first derivative of $f(x)$:
$$\eqalign{ f'(x) &= 0\ {\rm for}\ x < 0 \cr &= 4x
\ {\rm for}\ x\geq 0}$$
I observe that for $x = 0$, $f'(x)$ is $0$ both from the first
and from the second form of $f(x)$, that is on both sides of the
origin. So the first derivative $f'(0)=0$ exists at $x=0$. Hence
the graph of $f(x)$ has the tangent at $y=0$ at the origin.
Now, I calculate the second derivative:
$$\eqalign{ f''(x) &= 0\ for\ x < 0 \cr &= 4\ for \
x> 0.}$$
Hence the second derivative does not exist at the origin
because on the left the limiting value of $f''(x)$ as $x\to 0$ is
$0$ whereas on the right the limiting value of $f''(x)$ as $x\to 0$
is $4$. So there isn't a unique tangent to the graph of $f'(x)$ at
$x = 0$.
You may also like
Power Up
Show without recourse to any calculating aid that 7^{1/2} + 7^{1/3} + 7^{1/4} < 7 and 4^{1/2} + 4^{1/3} + 4^{1/4} > 4 . Sketch the graph of f(x) = x^{1/2} + x^{1/3} + x^{1/4} -x

