Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Published 2011 Revised 2017
Golden Mathematics
Setting Out on a Voyage of Exploration
 |
The connection between these pictures is a mathematical constant called the golden ratio or the divine proportion which often appears in mathematics, nature and art. The idea of this article is to map out for you, and guide you through, a sequence of NRICH challenges in which you can learn some mathematics by exploring the amazing properties of the golden ratio and Fibonacci numbers. You
will find Hints and Notes to help you. Try to solve the problems by your own methods before looking at the published solutions which have been written by school students.
There are some side trips to explore properties of the Fibonacci numbers which are not essential for the main voyage of discovery. You can take these side trips if you have time or maybe return to them later. |
|
The first two terms are 1 and 1 and the sequence starts 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
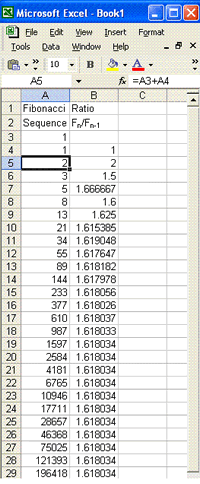
Now divide each term by the term before it and keep doing this for say 13 terms or more. What do you notice? Set up a spreadsheet like the one illustrated. One cell in the spreadsheet is outlined and you can see that the formula '=A3+A4' has been defined for that cell. The Fibonacci sequence has been produced by copying the formula down the column. In your spreadsheet change the first two terms to any values you choose. What happens to the sequence? What happens to the ratio of successive terms? You will find that, whatever the first two terms in the sequence, the ratio of successive terms quickly approaches a constant value. A later challenge in this trail leads to a proof that this value is the golden ratio. |
 |
Detour 1 : to explore some Fibonacci number patterns
One Step Two Step
Try this challenge You can go downstairs one step or two steps at a time. In how many ways can you do this for 1, 2, 3, 4 ... or any number of steps?
Fibs
Here's a challenge Fibs that involves exploring general Fibonacci sequences where each term is the sum of the two terms before it but the two initial terms may be anything you choose them to be.
Return to the main trail
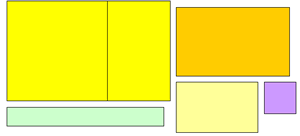 |
Here are some rectangles. The yellow, orange and cream rectangles are similar in more than colour, they are mathematically similar, in fact they are enlargements of each other. The other two rectangles are different, the blue rectangle is longer and thinner in shape and the lilac rectangle is more square. How do you tell from the measurements of any pair of rectangles whether they are similar? The answer is you tell from the proportions of the rectangles. Divide the length of the long side by the length of the short side and if these ratios are the same then the rectangles are similar. |
One rectangular shape is said to have 'divine proportions' and it is called the Golden Rectangle. If you cut off a square from a Golden Rectangle the remaining smaller rectangle has exactly the same proportions and the ratio of the long side to the short side is the golden ratio.
| For the next challenge you will need some squared paper. Draw bigger and bigger rectangles by adding on squares whose side lengths are the Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13, ... etc. Start with two unit squares side by side as in the diagram. Then draw below a square of side 2 units to make a 3 by 2 rectangle, then on the left a square of side 3 units to make a 5 by 3 rectangle, then above a square of side 5 units to make an 8 by 5 rectangle. | 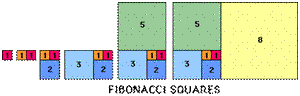 |
 |
Continue in this way, building on the squares in a clockwise pattern. On a sheet of 5mm squared paper, taking 5 mm as the unit, you can just fit a rectangle of side 55 by 34.
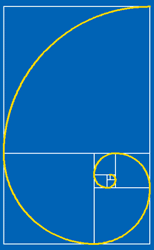
Imagine drawing these rectangles on a large tiled courtyard so that you can go on making bigger and bigger rectangles. Notice that the sides of these rectangles are the Fibonacci numbers and as you draw bigger rectangles they get closer in proportions to the Golden Rectangle. Now draw a spiral starting in the bottom left hand corner of the unit square on the left; draw a smoothly curving arc to the opposite corner of the square, move into and across the next square in a smoothly curving arc, and so on across each square. This is called a logarithmic spiral. In a section of a Nautilus shell, in the arrangements of seeds on flower heads and in the segments of a pine cone we can see similar spirals. |
|
Take a strip of paper and loosely tie a simple knot, then very carefully adjust it so that it is perfectly symmetrical before you flatten it so that it forms a pentagon. Can you prove that this is a regular pentagon? Hold it up to the light. Can you see a five pointed star or pentagram inside your pentagon?
Now draw a regular pentagon using a ruler and a protractor to measure the angles of 108 degrees. Draw in the five chords to form a pentagram star inside your pentagon. Measure the length of one of the chords and the length of a side of the pentagon and divide the chord length by the side length. You should get a ratio about 1.62 and later we'll prove that the exact value of this ratio is the golden ratio. |
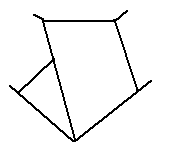 |
How many isosceles triangles with two angles of 36 degrees and one of 108 degrees can you find in your diagram? How many isosceles triangles with two angles of 72 degrees and one of 36 degrees can you find? These are golden triangles. Measure the ratio of the longest side to the shortest side in these triangles and you will again find that this is the golden ratio.
Inside your pentagram star there is a regular pentagon and if you draw the diagonals in this pentagon they form a smaller pentagram with an even smaller pentagon inside. You could continue this process indefinitely seeing pentagrams inside pentagons with pentagrams inside them and so on for ever.
Golden Construction
The next challenge is the Golden Construction. Have a go at this ruler and compass construction of a golden rectangle. If you cut off a square from a golden rectangle the remaining smaller rectangle has exactly the same proportions and the ratio of the long side to the short side is the golden ratio which you can find by this construction without using any algebra. To proceed further you need to be able to solve quadratic equations. You might want to come back to this trail when you have learnt some more algebra but finish now by reading some NRICH articles written for younger readers about the history of Fibonacci:
Fibonacci's Three Wishes.
Fibonacci's Three Wishes 2.
Leonardo of Pisa and the Golden Rectangle.
Second stage of the expedition
The golden rectangle has sides in the ratio $x:1$ such that, taking the shorter side length as one unit, when a square of side 1 unit is removed, the new rectangle, with sides of length $x-1$ and 1 units, has the same proportions. That is $${x\over 1} = {1\over x-1}.$$ Simplifying this expression we get the quadratic equation $x^2 - x - 1 = 0$ which has solutions $x = (1 \pm \sqrt 5)/2$. Thus the golden ratio, which is denoted by the Greek letter phi written $\phi$ must be the positive root $(1+\sqrt 5)/2 = 1 .618033\ldots$ and $1/\phi = \phi - 1 = 0.618033\ldots$.
The Golden Mean
The golden ratio features in Euclid's Elements (c.300 BC) as the extreme and mean ratio. It was studied earlier by Plato and the Pythagoreans and it appears even earlier in Egyptian architecture, for example in the Great Pyramid of Giza built around 2560 BC. The term 'golden' and the use of $\phi$ as the notation were introduced in the 19th and 20th centuries.

A point on a line segment dividing it into two lengths $a$ and $b$ is said to divide it externally in the ratio $a+b$ to $a$ and internally in the ratio $a$ to $b$. If these ratios are equal then the point is called the golden mean and the ratios are referred to as the extreme and mean ratios. Here $${a+b \over a} = {a\over b}$$ and writing $a/b = x$ we get $$1 + {1\over x} = x$$ giving the quadratic equation $x^2 - x -1 = 0$ whose positive solution is the golden ratio $\phi = (1 + \sqrt 5)/2$.
Golden Thoughts
The next challenge Golden Thoughts involves areas of triangles and the golden mean. It is by no means obvious, but easy enough to prove, that drawing three right angled triangles of equal area in a rectangle produces golden mean points on the sides of the rectangle.
Golden Eggs and Nested Roots
Here are two more problems to crack. One involves the area of an ellipse and the second involves infinitely many nested square roots. $$\phi = \sqrt{1+\sqrt{1+ \sqrt {1 + \sqrt {1 + ...}}}}$$
This infinitely long expression looks unmanageable at first but try squaring it.
Golden Triangles
In this challenge you meet golden triangles again and this time calculate the ratios which you found earlier by measurement and which give these triangles their special connection with the golden ratio.
Pentagons again
You have seen how the golden triangles fit into a regular pentagon. You can use what you have already learnt in Pent to prove that the ratio of the chord length to the side length is the golden ratio and that the points of intersection of the chords are the golden mean points.
The challenge Pentakite involves extending two edges of a pentagon to make a kite and an alternative way of calculating the the chord length.
The golden triangles in these diagrams give us exact values for some of the trigonometric ratios, namely $$\cos 36^o=\sin 54^o=\phi /2 = (1+\sqrt 5)/4$$ $${\rm sec} 72^o= {\rm cosec} 18^o=2\phi= (1+\sqrt 5)$$ and $$\cos 72^o=\sin 18^o=1/2\phi = (\sqrt 5 - 1)/4.$$
Golden Powers
Moving from geometry to algebra the next challenge Golden Powers involves powers of the golden ratio. You know $\phi^2 = \phi + 1$ so the challenge is to express the powers of $\phi$ in terms of $\phi$ and to find the values of $a_n$ and $b_n$ such that $\phi^n = a_n \phi + b_n$.
Detour 2 : A side expedition to explore Fibonacci Numbers
Golden Fibs
When is a Fibonacci sequence also a geometric sequence? Clearly this is not the case for the standard Fibonacci sequence but consider all sequences obeying the rule that each term is the sum of the two previous terms but with different initial terms. In Golden Fibs you will find a general Fibonacci sequence which is also a geometric sequence.
Gnomons
A gnomon is an L shaped carpenter's tool still used today which appeared often in Babylonian and Greek mathematics. Each Fibonacci number can be represented by a gnomon and the first of these two challenges involves an interactivity where you move the gnomons to join pairs together to make the next Fibonacci number in the sequence and of course you can cut your own from squared paper.
Fibonacci Factors
This challenge Fibonacci Factors is another digression about the Fibonacci sequence and here you will explore the patterns of multiples of 2 and 3 in the sequence.
Return to the Main Trail : Pythagorean Golden Means
Pythagorean Golden Means links Pythagoras' theorem and the arithmetic, geometric and harmonic means of two numbers specially chosen so that these three means are the lengths of the sides of a right-angled triangle. What is special about the numbers? You have guessed it! The ratio of one to the other involves the golden ratio but this time a power of the golden ratio.
Golden Fractions
Here you will learn about continued fractions, so called because they contain fractions within fractions going on for ever. The very simplest continued fraction has ones everywhere and its value is, surprise surprise, the golden ratio. Tackle the Golden Powers challenge to find out all about it.
Gold Medal
If you have worked through all these challenges then you deserve a gold medal, in the shape of a pentagon containing a star perhaps. You are now very knowledgeable about Fibonacci sequences and the golden ratio but did you know that new research results are being discovered every year and there is a mathematical journal called Fibonacci devoted entirely to newly discovered mathematics in this area.
For more reading on the subject and to learn more mathematics here are some links.
The article on the Golden Ratio, Fibonacci Numbers and Continued Fractions proves the result you discovered when working on Sheep Talk at the start of this trail and takes the ideas you have met on the trail a little further. It also introduces the use of two by two matrices to solve simultaneous equations and cobweb diagrams to find the limit of an iterative process.
Here is some more reading on the subject from the Plus maths website:
The life and numbers of Fibonacci.
The golden ratio and aesthetics by Mario Livio.
Maths and Art : a whistlestop tour.
and some book reviews:
The Golden Section by Mark Wainwright.
The Golden Ratio by Mario Livio.
You may also like
Continued Fractions I
An article introducing continued fractions with some simple puzzles for the reader.
Fibonacci Factors
For which values of n is the Fibonacci number fn even? Which Fibonnaci numbers are divisible by 3?

