Number Differences
Number Differences
Number Differences printable sheet
You might like to try A Ring of Numbers and More Rings of Numbers before this problem.
Place the numbers from 1 to 9 in the squares below so that the difference between joined squares is odd. (You must use each of the numbers once.)
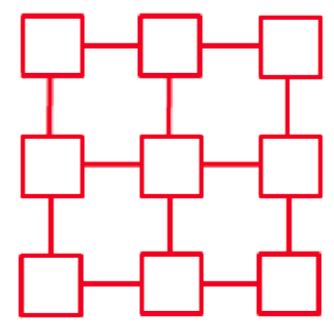
Can you find some other ways to do this?
Can you put the numbers in the squares so that the difference between joined squares is even? Explain your answer.
What general statements can you make about odd and even numbers?
This problem is based on an idea taken from "Apex Maths Pupils' Book 2" by Ann Montague-Smith and Paul Harrison, published in 2003 by Cambridge University Press.
Why do this problem?
This problem encourages pupils to form early stages of proof by using their knowledge of odd and even numbers to construct mathematical arguments. It is a good context for generalisations.
Possible approach
Ideally, this activity should follow on from Ring A Ring of Numbers and More Numbers in the Ring so that minimal introduction will be needed. However, if learners have not worked on the previous two tasks, you could show
them the grid on the interactive whiteboard and write in numbers (in whatever way you like) and ask them to talk to a neighbour about what they see. Sharing children's observations is likely to bring up odd and even numbers so that you can offer the challenge as it is written.
Give pairs time to work on the activity and draw the whole group together when appropriate to share any insights. It may be useful for children to have a sheet with blank grids in order to try out their ideas. Digit cards would also be handy.
You might like to invite children to find more than one way of arranging the digits for odd differences. When it comes to the challenge of arranging the digits so that the difference between joined numbers is even, look out for those children who have a hunch it is impossible. Encourage them to articulate why they think it cannot be solved. You may find that a whole-group
discussion is a fruitful way of coming to a good explanation.
Key questions
What have you tried so far?
Are there any other ways to do it?
How do you know this is impossible? Perhaps we just haven't found the one way that works?
Possible extension
You can assess children's understanding of the situation by giving them a new set of numbers to arrange. For example, what would happen with 2, 3, 4, 5, 6, 7, 8, 9 and 10? Are there any sets of numbers that would make both parts of the problem possible? This will encourage them to generalise the situation beyond numbers 1 to 9.
Alternatively, you may like to probe children's understanding of the way odd and even numbers behave. How do they know that two odd numbers will always have an even difference? Can they convince you that it will always be the case? They may well be able to create pictures that form a proof.
Possible support
Many children will find it beneficial to work on Ring A Ring of Numbers and More Numbers in the Ring before tackling this problem.
Related Collections
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Roll These Dice
Roll two red dice and a green dice. Add the two numbers on the red dice and take away the number on the green. What are all the different possible answers?
