Skip over navigation
The Fibonacci sequence is defined by the recurrence relation (sometimes called 'difference equation') $$F_n + F_{n+1}=F_{n+2}.$$ This is the simplest possible second order recurrence relation with constant coefficients as all the coefficients are one. The method of solving recurrence relations like this is to let $F_n=x^n$. Then $x^n+x^{n+1}=x^{n+2}$ and hence (dividing by $x^n$), $1 + x = x^2$ giving the quadratic equation $x^2-x-1=0$. So the quadratic equation has solutions $x={1 \pm \sqrt5\over 2}$. Hence the solutions of the recurrence relation are $$F_n=A\left({1+\sqrt5\over 2}\right)^n +B \left({1-\sqrt 5\over 2}\right)^n$$ where we have to find the values of the constants $A$ and $B$.
Putting $n=1$ and $F_1 = 1$ and multiplying by 2 $$2 = A(1 + \sqrt 5)+B(1-\sqrt 5)$$ and putting $n=2$ and $F_2=1$ and multiplying by 4 $$ 4 = A(1 + \sqrt 5)^2 + B(1-\sqrt 5)^2.$$ Solving these simultaneous equations for $A$ and $B$ we get $$A={1\over \sqrt 5}, \quad B =-{1\over \sqrt 5}.$$ Hence the solution of the recurrence relation is $$F_n = {1\over \sqrt 5}\left({1+\sqrt 5\over 2}\right)^n - {1\over \sqrt 5}\left(1-\sqrt 5\over 2\right)^n.$$ \par Note that the formula for $F_n$ is given in terms of the roots of the quadratic equation $x^2-x-1=0$ and one of the roots is the Golden Ratio which accounts for the many connections between Fibonacci numbers and the Golden Ratio.
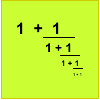

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Pythagorean Fibs
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Teachers' Resources
The Fibonacci sequence is defined by the recurrence relation (sometimes called 'difference equation') $$F_n + F_{n+1}=F_{n+2}.$$ This is the simplest possible second order recurrence relation with constant coefficients as all the coefficients are one. The method of solving recurrence relations like this is to let $F_n=x^n$. Then $x^n+x^{n+1}=x^{n+2}$ and hence (dividing by $x^n$), $1 + x = x^2$ giving the quadratic equation $x^2-x-1=0$. So the quadratic equation has solutions $x={1 \pm \sqrt5\over 2}$. Hence the solutions of the recurrence relation are $$F_n=A\left({1+\sqrt5\over 2}\right)^n +B \left({1-\sqrt 5\over 2}\right)^n$$ where we have to find the values of the constants $A$ and $B$.
Putting $n=1$ and $F_1 = 1$ and multiplying by 2 $$2 = A(1 + \sqrt 5)+B(1-\sqrt 5)$$ and putting $n=2$ and $F_2=1$ and multiplying by 4 $$ 4 = A(1 + \sqrt 5)^2 + B(1-\sqrt 5)^2.$$ Solving these simultaneous equations for $A$ and $B$ we get $$A={1\over \sqrt 5}, \quad B =-{1\over \sqrt 5}.$$ Hence the solution of the recurrence relation is $$F_n = {1\over \sqrt 5}\left({1+\sqrt 5\over 2}\right)^n - {1\over \sqrt 5}\left(1-\sqrt 5\over 2\right)^n.$$ \par Note that the formula for $F_n$ is given in terms of the roots of the quadratic equation $x^2-x-1=0$ and one of the roots is the Golden Ratio which accounts for the many connections between Fibonacci numbers and the Golden Ratio.
This problem complements the material in the article
For a sequence of, mainly more elementary, problems on these topics see Golden Mathematics
You may also like
Continued Fractions I
An article introducing continued fractions with some simple puzzles for the reader.
Fibonacci Factors
For which values of n is the Fibonacci number fn even? Which Fibonnaci numbers are divisible by 3?

