Skip over navigation
We can show that $14^2 = 196$ by considering the area of a $14$ by $14$ square:
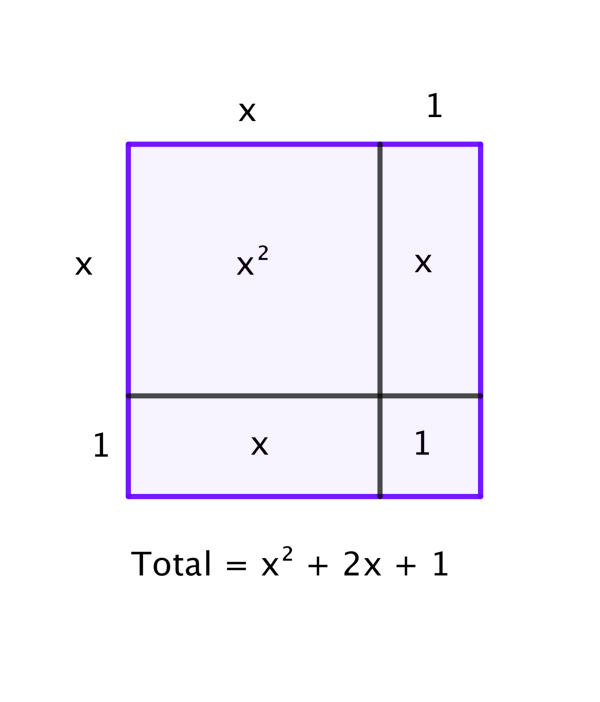
We can show that $(x + 1)^2 \equiv x^2 + 2x + 1$ by considering the area of an $(x + 1)$ by $(x + 1)$ square:
Show in a similar way that $(x + 2)^2 \equiv x^2 + 4x + 4$.
Then use the same method to evaluate $(x + 3)^2$ and $(x + a)^2$.
Partitioning Revisited
Age 11 to 14
Challenge Level 
We can show that $14^2 = 196$ by considering the area of a $14$ by $14$ square:
We can show that $(x + 1)^2 \equiv x^2 + 2x + 1$ by considering the area of an $(x + 1)$ by $(x + 1)$ square:
Show in a similar way that $(x + 2)^2 \equiv x^2 + 4x + 4$.
Then use the same method to evaluate $(x + 3)^2$ and $(x + a)^2$.
You may also like
Cubes Within Cubes Revisited
Imagine starting with one yellow cube and covering it all over with a single layer of red cubes, and then covering that cube with a layer of blue cubes. How many red and blue cubes would you need?