Skip over navigation
These printable worksheets may be useful: Quadrilaterals Game
Quadrilaterals Game Cards
There is an excellent article by Gillian Hatch on the NRICH site, Using Games in the Classroom
She analyses what goes on when geometrical mathematical games are used as a pedagogic device.
These are the headings from the article:
Learning
A game can generate an unreasonable amount of practice
Geometric games create a context for using geometric reasoning
A game will often result in the making of generalised statements
A game can allow the introduction of ideas that are difficult to develop in other ways.
Games seem to be able to lead pupils to work above their normal level
Ways of working
A game leads pupils to talk mathematics
A game can create discussion of all kinds
Games put pressure on players to work mentally
A game does not define the way in which a problem is to be solved or worked out
A game often can be played at more then one level
Pupil experience
It is acceptable to learn the rules of a game gradually
Games are played in a context in which there is usually unthreatening help available
The pieces used in a game are concrete objects
A game allows a pupil to hide until he feels confident
Quadrilaterals Game
Age 11 to 14
Challenge Level 
These printable worksheets may be useful: Quadrilaterals Game
Quadrilaterals Game Cards
Why play this game?
This game fits in well into a unit of work on the properties of polygons, that could also include the problems Property Chart and Shapely PairsThere is an excellent article by Gillian Hatch on the NRICH site, Using Games in the Classroom
These are the headings from the article:
Learning
A game can generate an unreasonable amount of practice
Geometric games create a context for using geometric reasoning
A game will often result in the making of generalised statements
A game can allow the introduction of ideas that are difficult to develop in other ways.
Games seem to be able to lead pupils to work above their normal level
Ways of working
A game leads pupils to talk mathematics
A game can create discussion of all kinds
Games put pressure on players to work mentally
A game does not define the way in which a problem is to be solved or worked out
A game often can be played at more then one level
Pupil experience
It is acceptable to learn the rules of a game gradually
Games are played in a context in which there is usually unthreatening help available
The pieces used in a game are concrete objects
A game allows a pupil to hide until he feels confident
You may also like
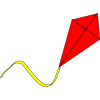
Linkage
Four rods, two of length a and two of length b, are linked to form a kite. The linkage is moveable so that the angles change. What is the maximum area of the kite?
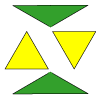
Making Rectangles, Making Squares
How many differently shaped rectangles can you build using these equilateral and isosceles triangles? Can you make a square?
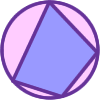
The Cyclic Quadrilateral
This gives a short summary of the properties and theorems of cyclic quadrilaterals and links to some practical examples to be found elsewhere on the site.